题目内容
2.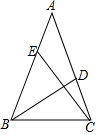 如图,在△ABC中,AB=AC,∠ABC的平分线交AC于点D,CE⊥BD交AB于点E,∠BEC=54°,则∠ACE的度数为( )
如图,在△ABC中,AB=AC,∠ABC的平分线交AC于点D,CE⊥BD交AB于点E,∠BEC=54°,则∠ACE的度数为( )| A. | 54° | B. | 36° | C. | 18° | D. | 16° |
分析 根据等腰三角形的性质得到∠ABC=∠ACB,根据三角形的内角和得到∠A=180°-∠ABC-∠ACB=180°-2∠ABC,由角平分线的定义得到∠DBC=$\frac{1}{2}$∠ABC,列方程即可得到结论.
解答 解:∵AB=AC,
∴∠ABC=∠ACB,
∴∠A=180°-∠ABC-∠ACB=180°-2∠ABC,
∵∠ABC的平分线交AC于点D,
∴∠DBC=$\frac{1}{2}$∠ABC,
∵CE⊥BD,
∴∠ECB=90°-∠DBC=90°-$\frac{1}{2}$∠ABC,
∴∠ACE=∠ACB-∠ECB=∠ABC-90°+$\frac{1}{2}$∠ABC,
∵∠BEC=∠A+∠ACE=180°-2∠ABC+∠ABC-90°+$\frac{1}{2}$∠ABC=54°,
∴∠ABC=72°,
∴∠A=36°,
∴∠ACE=18°.
故选C.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形额外角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
12.一个等腰三角形的一边长为6cm,周长为30cm,则它的另两边长分别为( )
| A. | 6cm,18cm | B. | 12cm,12cm | ||
| C. | 6cm,12cm | D. | 6cm,18cm或12cm,12cm |
10.一组数据:3,2,1,2,2的众数,中位数分别是( )
| A. | 2,1 | B. | 2,2 | C. | 3,1. | D. | 2,1 |
7.若分式$\frac{{a}^{2}-1}{{a}^{2}+1}$的值为0,则( )
| A. | a=-1 | B. | a=±1 | C. | a=1 | D. | a≠1 |
14.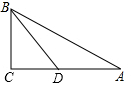 如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为( )
如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为( )
 如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为( )
如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为( )| A. | 4 | B. | 3 | C. | 2.5 | D. | 5 |
 如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有①②③④.(请填序号)
如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有①②③④.(请填序号) 如图是由若干个大小相同的小正方体搭成的几何体,每个小正方体的棱长都为1.
如图是由若干个大小相同的小正方体搭成的几何体,每个小正方体的棱长都为1. 如图,甲、乙两个转盘转动一次,最终指针指向红色区域是(填“是”或“不是”)等可能性事件.
如图,甲、乙两个转盘转动一次,最终指针指向红色区域是(填“是”或“不是”)等可能性事件.