题目内容
9.已知等腰三角形ABC和DBE的底角共顶点,AB=AC,DB=DE,∠BAC=∠BDE,以线段AD和AC为邻边作?ACFD,连接CE.(1)如图1,B、D、C依次在同一条直线上,若∠BAC=∠BDE=60°,则∠ECF=60°.
(2)如图2,B、D、C依次在同一条直线上,若∠BAC=∠BDE=90°,则∠ECF=45°.
请你完成(1)、(2)两个命题,并从中任选一个进行证明.
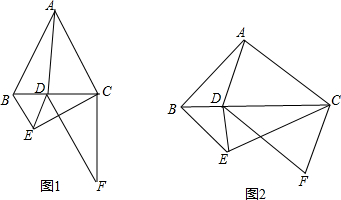
分析 (1)由已知条件得到△ABC与△BDE是等边三角形,推出△ABD≌△BCE,根据全等三角形的性质得到∠BAD=∠BCE,由四边形ADFC是平行四边形,得到AD∥CF,根据平行线的性质得到∠ADC=∠DCF,由外角的性质得到∠ADC=∠ABC+∠BAD,∠DCF=∠BCE+∠ECF,即可得到结论.
(2)由已知条件得到△ABC与△BDE是等腰直角三角形,求得AB=$\frac{\sqrt{2}}{2}$BC,BE=$\frac{\sqrt{2}}{2}$BD,∠ABC=∠DBE=45°,推出△ABD∽△BCE,根据相似三角形的性质得到∠ADC=∠DCF,由外角的性质得到∠ADC=∠ABC+∠BAD,∠DCF=∠BCE+∠ECF,即可得到结论.
解答 解:(1)∵AB=AC,DB=DE,∠BAC=∠BDE=60°,
∴△ABC与△BDE是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°,
在△ABD与△BCE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠DBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△BCE,
∴∠BAD=∠BCE,
∵四边形ADFC是平行四边形,
∴AD∥CF,
∴∠ADC=∠DCF,
∵∠ADC=∠ABC+∠BAD,∠DCF=∠BCE+∠ECF,
∴∠ECF=∠ABC=60°,
故答案为:60°;
(2)∵AB=AC,DB=DE,∠BAC=∠BDE=90°,
∴△ABC与△BDE是等腰直角三角形,
∴AB=$\frac{\sqrt{2}}{2}$BC,BE=$\frac{\sqrt{2}}{2}$BD,∠ABC=∠DBE=45°,
∴$\frac{AB}{BC}=\frac{BE}{BD}$,
∴△ABD∽△BCE,
∴∠ADC=∠DCF,
∵四边形ADFC是平行四边形,
∴AD∥CF,
∴∠ADC=∠DCF,
∵∠ADC=∠ABC+∠BAD,∠DCF=∠BCE+∠ECF,
∴∠ECF=∠ABC=45°,
故答案为:45°.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的性质,等边三角形的性质,等腰直角三角形的性质,熟练掌握全等三角形的性质是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
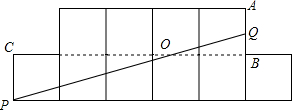 如图是由10个边长为1的小正方形组成的图形,点P在一正方形的顶点,点Q在边AB上,PQ与BC交于点0,若PQ恰将这图形的面积平分,则$\frac{QO}{OP}$的值是$\frac{3}{5}$.
如图是由10个边长为1的小正方形组成的图形,点P在一正方形的顶点,点Q在边AB上,PQ与BC交于点0,若PQ恰将这图形的面积平分,则$\frac{QO}{OP}$的值是$\frac{3}{5}$.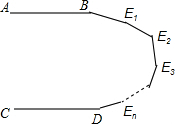 如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)
如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)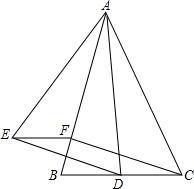 如图,△ABC中,AB=AC,△ABC∽△AED,且D是BC边上任意一点(不与点C重合),作EF∥BC交AB于点F.求证:四边形CDEF是平行四边形.
如图,△ABC中,AB=AC,△ABC∽△AED,且D是BC边上任意一点(不与点C重合),作EF∥BC交AB于点F.求证:四边形CDEF是平行四边形.