题目内容
4.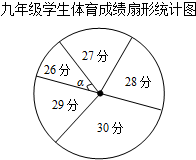 为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.| 九年级学生体育模考成绩统计表 | ||
| 体育成绩(分) | 人数(人) | 百分比(%) |
| 26 | 5 | 10 |
| 27 | m | 20 |
| 28 | 8 | 16 |
| 29 | 12 | 24 |
| 30 | 15 | |
(1)m=10;抽取的部分学生体育模考成绩的中位数为29;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
分析 (1)首先根据体育成绩是28分的有8人,所占的百分比是16%,即可求得总人数,然后根据百分比的意义求解;
(2)利用总人数500乘以对应的百分比即可求得.
解答 解:(1)调查的总人数是:8÷16%=50(人),
则体育成绩是26分的人数是:50×$\frac{36}{360}$=5,
体育成绩是29分的人数是:50×24%=12(人),
则m=50-5-8-12-15=10.
中位数是:29.
故答案是:10,29;
(2)随机抽取的学生是50人,模考成绩优秀的有27人.
∴$\frac{27}{50}$×500=270(人).
答:估计该校九年级学生体育模考成绩达到优秀的总人数约为270人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.如果正三角形的内切圆半径为1,那么这个正三角形的边长为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\sqrt{3}$ |
16.-2的绝对值是( )
| A. | ±2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |




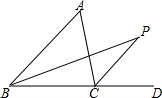 如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.
如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.