题目内容
7.老师在黑板上出了一道解方程的题$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$,小明马上举手,要求到黑板上做,他是这样做的:4(2x-1)=1-3(x+2)①
8x-4=1-3x-6②
8x+3x=1-6+4③
11x=-1④
x=-$\frac{1}{11}$⑤
(1)老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在第步(填编号);
(2)请你自己细心地解下面的方程:2x-$\frac{5x-2}{3}$=4-$\frac{3x+1}{2}$.
分析 (1)观察小明解方程过程,找出出错步骤即可;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)第①步去分母出错;
(2)去分母得:12x-2(5x-2)=24-3(3x+1),
去括号得:12x-10x+4=24-9x-3,
移项合并得:11x=17,
解得:x=$\frac{17}{11}$.
点评 此题考查了解一元一次方程,去分母时等式两边各项都有乘以各分母的最小公倍数.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 单项式是整式,整式也是单项式 | |
| B. | 25与x5是同类项 | |
| C. | 单项式-$\frac{1}{2}$πx3y的系数是-$\frac{1}{2}$π,次数是4 | |
| D. | $\frac{1}{x}$+2是一次二项式 |
12.计算tan30°的值等于( )
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.下列说法:
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
其中说法正确的是( )
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
其中说法正确的是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
17.一次函数图象过点(0,2)和(4,0),其函数表达式为( )
| A. | y=$\frac{1}{2}$x+2 | B. | y=2x+4 | C. | y=-2x+2 | D. | y=-$\frac{1}{2}$x+2 |
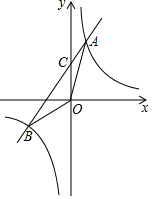 如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:
如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: