题目内容
15.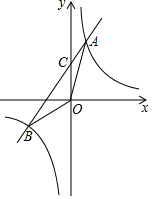 如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:
如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出使反比例函数的值大于一次函数的值的x的取值范围.
分析 (1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;
(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;
(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.
解答 解:(1)令反比例函数y=$\frac{8}{x}$,x=2,则y=4,
∴点A的坐标为(2,4);
反比例函数y=$\frac{8}{x}$中y=-2,则-2=-$\frac{8}{x}$,解得:x=-4,
∴点B的坐标为(-4,-2).
∵一次函数过A、B两点,
∴$\left\{\begin{array}{l}{4=2k+b}\\{-2=-4k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴一次函数的解析式为y=x+2.
(2)设直线AB与y轴交于C,
令为y=x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB=$\frac{1}{2}$OC•(xA-xB)=$\frac{1}{2}$×2×[4-(-2)]=6.
(3)观察函数图象发现:
当x<-4或0<x<2时,反比例函数图象在一次函数图象上方,
∴反比例函数的函数值大于一次函数的函数值时x的取值范围为x<-4或0<x<2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出点A、B的坐标;(2)找出点C的坐标;(3)根据函数图象的上下关系解决不等式.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.

 名校课堂系列答案
名校课堂系列答案| A. | 带正号的数是正数 | B. | 带负号的数是负数 | ||
| C. | 负数一定带有负号 | D. | 正数一定带有正号 |
| A. | 在一次抽奖活动中,“中奖的概率是$\frac{1}{100}$”表示抽奖l00次就一定会中奖 | |
| B. | 某市“明天降雨的概率是75%”表示明天有75%的时间会降雨 | |
| C. | 随机抛掷一枚均匀的硬币,落地后正面一定朝上 | |
| D. | 在平面内,平行四边形的两条对角线一定相交 |
 如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE.
如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE. 如图是一个破残的车轮,请用尺规作图法补全车轮并标出圆心O.
如图是一个破残的车轮,请用尺规作图法补全车轮并标出圆心O.