题目内容
已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点（A在B的左边），与y轴交于点C．
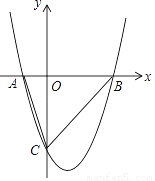
（1）求出点A、B、C的坐标．
（2）求S△ABC
（3）在抛物线上（除点C外），是否存在点N，使得S△NAB=S△ABC ， 若存在，求出点N的坐标，若不 存在，请说明理由．
（1）A（﹣1，0）、B（3，0）；（2）6；（3）存在，点N的坐标（1+ ，3）或（1﹣，3）或（2，﹣3） 【解析】试题分析： （1）在解析式中，由，求得的对应值可得点C的坐标；由，求得对应的的值可得点A、B的坐标； （2）根据（1）中所求点A、B、C坐标可求得△ABC的面积； （3）设点N的纵坐标为，则由S△NAB=S△ABC可知或，由点N在抛物线上，可得或，解方程即...
练习册系列答案
相关题目
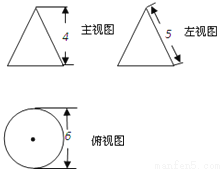
倍的相反数”：_____．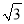
，沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°，（坡度i=1： 
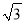是指坡面的铅直高度FE与水平宽度DE的比）．请你计算出该建筑物BC的高度．（取
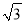=1.732，结果精确到0.1m）．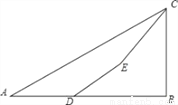
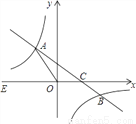
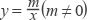的图象交于二四象限内的A、B 两点，与x轴交于C点，点B的坐标为（6，n），线段OA=5，E为x轴负半轴上一点，且sin∠AOE=
．
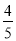