题目内容
18.观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…则81+82+83+84…+82015的和的个位数字是4.分析 首先根据81=8,82=64,83=512,84=4096,85=32768,86=262144,…,可得81、82、83、84、…、8n的个位上的数字每4个数字一个循环,它们分别为:8、4、2、6;然后用2015除以4,判断出一共有503个循环,剩下的三个数的个位数分别是8、4、2,最后用每个循环的4个数的和乘以循环数,再加上8、4、2的和,判断出81+82+83+84…+82015的和的个位数字是多少即可.
解答 解:∵81=8,82=64,83=512,84=4096,85=32768,86=262144,…,
∴81、82、83、84、…、8n的个位上的数字每4个数字一个循环,它们分别为:8、4、2、6;
2015÷4=503…3,
∵(8+4+2+6)×503+(8+4+2)
=20×503+14
=10060+14
=10074
∴81+82+83+84…+82015的和的个位数字是4.
故答案为:4.
点评 此题主要考查了尾数的特征,要熟练掌握,解答此题的关键是要明确:81、82、83、84、…、8n的个位上的数字每4个数字一个循环,它们分别为:8、4、2、6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.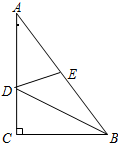 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )| A. | $\frac{\sqrt{10}}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{3}{2}$ |
3.在一个不透明的袋子中,装有红球、黄球、篮球、白球各1个,这些球除颜色外无其他差别,从袋中随机取出一个球,取出红球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
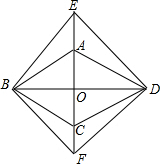 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.