题目内容
8.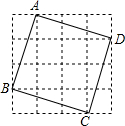 如图,由16个边长为1的小正方形构成的网格图中,有一个正方形(图中实线表示)
如图,由16个边长为1的小正方形构成的网格图中,有一个正方形(图中实线表示)(1)请你计算这个正方形的面积和边长;
(2)这个正方形的边长介于哪两个整数之间?
分析 (1)正方形的面积等于大正方形的面积减去4个直角三角形的面积,由勾股定理求出正方形的边长即可;
(2)由$\sqrt{9}$<$\sqrt{10}$<$\sqrt{16}$,即可得出结果.
解答 解:(1)正方形的面积=42-4×$\frac{1}{2}$×1×3=10;
正方形的边长=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
(2)∵$\sqrt{9}$<$\sqrt{10}$<$\sqrt{16}$,
∴3<$\sqrt{10}$<4,
即正方形的边长介于3和4两个整数之间.
点评 本题考查了勾股定理、估算无理数的大小、正方形的性质;熟练掌握正方形的性质,由勾股定理求出正方形的边长是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.
若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.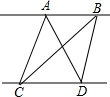 如图,已知AB∥CD,S△ACD=6cm2,则S△BCD=6cm2.
如图,已知AB∥CD,S△ACD=6cm2,则S△BCD=6cm2.