题目内容

3．四边形的四个顶点为A（6.6），B（-4，3），C（-1，-7），D（9，-4），则其面积为109．

分析 根据S四边形ABCD=S四边形MNPQ-S△ABM-S△BNC-S△PDC-S△ADQ可得答案．

解答 解：如图所示：分别过A、C点作x轴的平行线，与过B、D平行于y轴的直线相交于M、N、P、Q，

S四边形ABCD=S四边形MNPQ-S△ABM-S△BNC-S△PDC-S△ADQ=13×13-$\frac{1}{2}$×10×3-$\frac{1}{2}$×10×3-$\frac{1}{2}$×10×3-$\frac{1}{2}$×10×3=109．
故答案为109．

点评 此题主要考查了坐标与图形的性质以及四边形面积求法，利用特殊图形面积差得出四边形面积是解题关键．

练习册系列答案
相关题目
13．如图，在△ABC中，AD⊥BC于点D，BD=CD，若BC=8，AD=6，则图中阴影部分的面积为12．
14．（1）代数式$1-\frac{3x-1}{2}$的值不大于$\frac{1-2x}{3}$的值，求x的范围．
（2）解不等式组$\left\{\begin{array}{l}2（x+2）≤3x+3\\ \frac{x}{3}＜\frac{x+1}{4}\end{array}\right.$，并判断x=$\frac{2}{3}$是否为此不等式组的解．
11．如图1，在等边△ABC中，E、D两点分别在边AB、BC上，BE=CD，AD、CE相交于点F．
（1）求∠AFC的度数；
（2）延长CE至点P，连接BP，如图2，∠BPC=30°，且CF=$\frac{2}{9}$CP，求$\frac{PF}{AF}$的值？
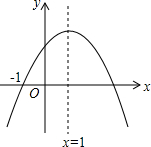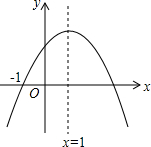18．已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（　　）
A．ac＞0B．当x＞1时，y随x的增大而增大
C．2a+b=1D．方程ax2+bx+c=0有一个根是x=3
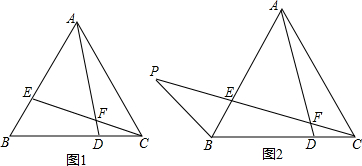
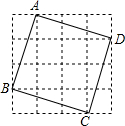8．如图，由16个边长为1的小正方形构成的网格图中，有一个正方形（图中实线表示）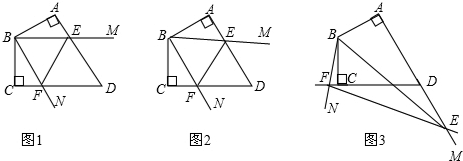
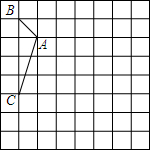（1）请你计算这个正方形的面积和边长；
（2）这个正方形的边长介于哪两个整数之间？
15．已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E、F．
（1）当∠MBN绕B点旋转到AE=CF时（如图1），试猜想AE，CF，EF之间存在怎样的数量关系？请将三条线段分别填入后面横线中：AE+CF=EF．（不需证明）
（2）当∠MBN绕B点旋转到AE≠CF（如图2）时，上述（1）中结论是否成立？请说明理由．
（3）当∠MBN绕B点旋转到AE≠CF（如图3）时，上述（1）中结论是否成立？若不成立，线段AE，CF，EF又有怎样的数量关系？请直接写出你的猜想，不需证明．
12．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，请按要求完成下列步骤：
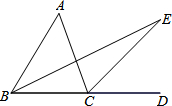（1）画出将△ABC绕点B按逆时针方向旋转90°后所得到的△A1BC1；
（2）求△ABC旋转到△A1BC1的过程中，点C所经过的路径长为2π；AC边扫过的图形面积为$\frac{7π}{2}$．
13．如图所示，∠ACD是△ABC的外角，∠A=40°，BE平分∠ABC，CE平分∠ACD，且BE、CE交于点E．则∠E=20度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网