题目内容
5.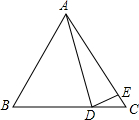 如图,△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
如图,△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
分析 在△ABD中,由内角和定理求得∠BDA=180°-(∠B+∠BAD)=75°,由平角定义知∠ADE=60°,再在△ADE中,由∠CAD=180°-∠ADE-∠AED可得答案.
解答 解:在△ABD中,∵∠B=65°,∠BAD=40°,
∴∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°,
∵∠CDE=45°,
∴∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°,
在△ADE中,∵∠AED=100°,
∴∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.
点评 本题主要考查三角形的内角和定理,掌握三角形内角和定理:三角形内角和是180°是解题的关键.

练习册系列答案
相关题目
16. 某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
(1)在频数分布表中,a=60,b=0.05;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
 某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
20.不等式组$\left\{\begin{array}{l}{2x+3<1}\\{2(x-2)>3x}\end{array}\right.$的解集是( )
| A. | x<-2 | B. | x<-4 | C. | -4<x<-2 | D. | 无解 |
10.洛宁县五月份连续五天的最高气温分别为30,27,27,28,33(单位℃),这组数据中的中位数和众数分别是( )
| A. | 29,33 | B. | 29,27 | C. | 30,27 | D. | 28,27 |
13.下列由左边到右边的变形,是因式分解的是( )
| A. | am+bm-1=m(a+b)-1 | B. | (x+2)(x-5)=x2-3x-10 | C. | x2+5x+4=x(x+5+$\frac{4}{x}$) | D. | x2-4x=x(x-4) |