题目内容
3. 如图,四边形ABCD的对角线AC,BD交于点O,EF过点O,若OA=OC,OB=OD,则图中全等的三角形有6对.
如图,四边形ABCD的对角线AC,BD交于点O,EF过点O,若OA=OC,OB=OD,则图中全等的三角形有6对.
分析 先根据平行四边形的性质及已知条件得到图中全等的三角形:△ADC≌△CBA,△ABD≌△CDB,△OAD≌△OCB,△OEA≌△OFC,△OED≌△OFB,△OAB≌△OCD共6对,再证明即可.
解答 解:①△ADC≌△CBA,∵ABCD为平行四边形,∴AB=CD,∠ABC=∠ADC,AD=BC,∴△ADC≌△CBA;
②△ABD≌△CDB,∵ABCD为平行四边形,∴AB=CD,∠BAD=∠BCD,AD=BC,∴△ABD≌△CDB;
③△OAD≌△OCB,∵对角线AC与BD的交于O,∴OA=OC,OD=OB,∠AOD=∠BOC,∴△OAD≌△OCB;
④△OEA≌△OFC,∵对角线AC与BD的交于O,∴OA=OC,∠AOE=∠COF,∠AOE=∠COF,∴△OEA≌△OFC;
⑤△OED≌△OFB,∵对角线AC与BD的交于O,∴OD=OB,∠EOD=∠FOB,OE=OF,∴△OED≌△OFB;
⑥△OAB≌△OCD,∵对角线AC与BD的交于O,∴OA=OC,∠AOB=∠DOC,OB=OD,∴△OAB≌△OCD.
故答案为6.
点评 本题考查平行四边形的性质及全等三角形的判定条件,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
15.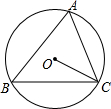 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )| A. | 15° | B. | 18° | C. | 20° | D. | 28° |
12.计算(a2)3的正确结果是( )
| A. | 3a2 | B. | a6 | C. | a5 | D. | 6a |
12.下列说法正确的是( )
| A. | 角的边越长,角度就越大 | B. | 周角就是一条射线 | ||
| C. | 一条直线可以看成平角 | D. | 平角的两边可以构成一条直线 |
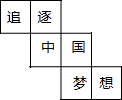 一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )
一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )