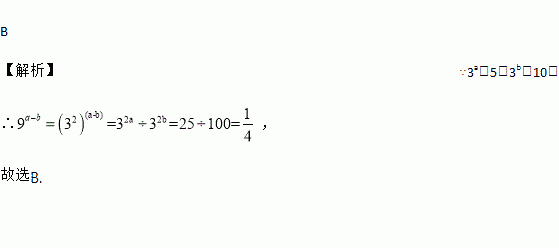题目内容
如果3a＝5，3b＝10，那么9a－b的值为( )
A.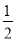 
B. 
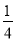C.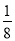 
D. 不能确定
B
【解析】∵3a＝5，3b＝10，
∴，
故选B.
练习册系列答案
相关题目
如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
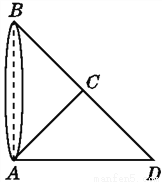
证明见解析.
【解析】试题分析：根据SAS即可证明△ACB≌△ACD，由此即可解决问题．
试题解析：因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD. 如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.
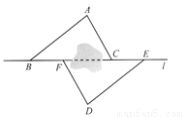
（1）求证：△ABC≌△DEF；
（2）指出图中所有平行的线段，并说明理由.
（1）详见解析；（2）∠ABC=∠DEF，∠ACB=∠DFE,理由见解析.
【解析】
试题分析：（1）理用SSS即可判定△ABC≌△DEF；（2）AB∥DE,AC∥DF,由全等三角形的性质可得∠ABC=∠DEF，∠ACB=∠DFE,根据平行线的性质即可得结论.
试题解析：（1）证明：∵BF=EC，
∴BF+CF=CF+CE，
∴BC=EF
∵AB=DE，AC=D... 在长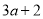为
，宽为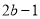
的长方形铁片上，挖去长为
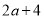，宽为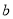
的小长方形铁片，求剩余部分面积。
4ab-3a-2
【解析】试题分析：根据长方形的面积=长×宽，利用大长方形的面积减去小长方形的面积即可.
试题解析：（3a+2）（2b-1）-（2a+4）b
=6ab+4b-3a-2-2ab-4b
=4ab-3a-2 若(2x＋1)0＝1，则x的取值范围是_____.
x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0，解得，所以当(2x＋1)0＝1，x的取值范围是. 若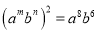
，那么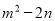
的值是 ( )
A. 10 B. 52 C. 20 D. 32
A
【解析】∵，
∴2m=8,2n=6，
即m=4，n=3，
∴=16-6=10.
故选A. 若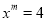
， 
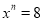，求
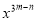的值。
8
【解析】试题分析：根据已知条件，逆用同底数幂的除法法则计算即可.
试题解析：
∵， ，
∴ 如果x2＋ax＋9＝(x＋3)2，那么a的值为( )
A. 3 B. ±3 C. 6 D. ±6
C
【解析】∵x2+ax+9=（x+3）2，而（x+3）2=x2+6x+9；即x2+ax+9=x2 
__________
， 
__________．
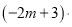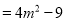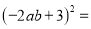【解析】试题解析：(1) 故填(?2m?3)；
故填
故答案为：(?2m?3)，