题目内容
15.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点B对应有理数b,且b-2a=7,则数轴上原点应是( )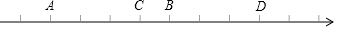
| A. | A 点 | B. | B 点 | C. | C 点 | D. | D点 |
分析 由数轴可知,b-a=4,又因为b-2a=7,所以可以求出a,b的值,进而可以确定原点的位置.
解答 解:观察数轴可得:B点在A点的右边且距离A点5个单位长度,
所以b-a=4①,
又因为b-2a=7②,
解由①②组成的方程组$\left\{\begin{array}{l}{b-a=4①}\\{b-2a=7②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=1}\end{array}\right.$,
所以点A表示的数是-3,点B表示的数是1,
所以数轴上原点应是点C.
故选C.
点评 此题考查了数轴,弄清题意是解本题的关键.

练习册系列答案
相关题目
6.下列说法中正确的个数有( )
(1)在同一平面内,不相交的两条直线必平行;
(2)两条直线第三条直线所截,同旁内角互补;
(3)相等的角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;
(5)经过直线外一点,有且只有一条直线与已知直线平行.
(1)在同一平面内,不相交的两条直线必平行;
(2)两条直线第三条直线所截,同旁内角互补;
(3)相等的角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;
(5)经过直线外一点,有且只有一条直线与已知直线平行.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.下列图象中,变量y不是变量x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
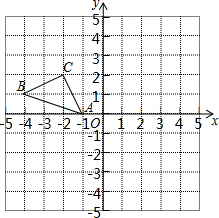 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: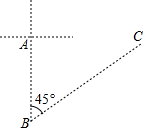 距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)
距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)
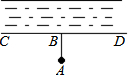 如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短.
如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短. 已知:如图,在△ABC中,∠ABC=∠ACB,BD⊥AC于D,点E在AB边上,CE交BD于点F,且∠BEF=∠BFE,EG⊥AC于点G.若GE=3,CD=4,则线段BE的长为7.
已知:如图,在△ABC中,∠ABC=∠ACB,BD⊥AC于D,点E在AB边上,CE交BD于点F,且∠BEF=∠BFE,EG⊥AC于点G.若GE=3,CD=4,则线段BE的长为7.