题目内容
5.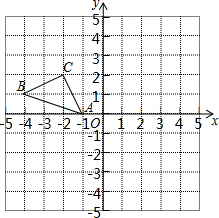 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:(1)作出△ABC绕点A逆时针旋转90°的△AB1C1;作出△ABC关于点A成中心对称的△AB2C2;
(2)点B1的坐标为(-2,-3);点C2的坐标为(-3,-1);
(3)若点P(a,b)是△ABC内任意一点,则点P在△AB2C2内的对应点的坐标为(a+6,-b).
分析 (1)先根据图形旋转的性质画出△AB1C1,再根据中心对称的性质画出△AB2C2即可;
(2)根据各点在坐标系中的位置写出点B1,C2的坐标即可;
(3)根据各点坐标的变化即可得出结论.
解答  解:(1)如图,△AB1C1与△AB2C2即为所求;
解:(1)如图,△AB1C1与△AB2C2即为所求;
(2)由图可知,B1(-2,-3),C2(-3,-1).
故答案为:(-2,-3),(-3,-1);
(3)∵B(-4,1),B2(2,-1),P(a,b)是△ABC内任意一点,
∴点P在△AB2C2内的对应点的坐标为(a+6,-b).
故答案为:(a+6,-b).
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下来根式中,为最简二次根式的是( )
| A. | $\sqrt{11}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
14.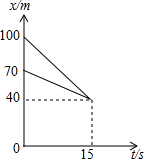 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )| A. | 灰太狼追上喜羊羊时,喜羊羊跑了60m | |
| B. | 喜羊羊与灰太狼最初的距离是30m | |
| C. | 灰太狼跑了60m追上了喜羊羊 | |
| D. | 灰太狼用15s追上了喜羊羊 |
15.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点B对应有理数b,且b-2a=7,则数轴上原点应是( )
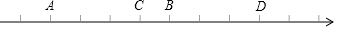
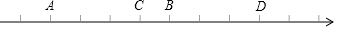
| A. | A 点 | B. | B 点 | C. | C 点 | D. | D点 |
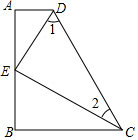 如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.