题目内容
3.圆的半径为1,AB是圆中的一条弦,AB=$\sqrt{3}$,则弦AB所对的圆周角的度数为60°或120°.分析 如图,作OH⊥AB于H,连接OA、OB,∠C和∠C′为AB所对的圆周角,根据垂径定理得到AH=BH=$\frac{1}{2}$AB=$\frac{\sqrt{3}}{2}$,则利用余弦的定义可得到∠OAH=30°,接着根据三角形内角和可计算出∠AOB=120°,然后根据圆周角定理和圆内接四边形的性质求出∠C和∠C′的度数即可.
解答 解: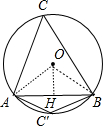 如图,作OH⊥AB于H,连接OA、OB,∠C和∠C′为AB所对的圆周角,
如图,作OH⊥AB于H,连接OA、OB,∠C和∠C′为AB所对的圆周角,
∵OH⊥AB,
∴AH=BH=$\frac{1}{2}$AB=$\frac{\sqrt{3}}{2}$,
在Rt△OAH中,∵cos∠OAH=$\frac{AH}{OA}$=$\frac{\sqrt{3}}{2}$,
∴∠OAH=30°,
∴∠AOB=180°-60°=120°,
∴∠C=$\frac{1}{2}$∠AOB=60°,
∴∠C′=180°-∠C=120°,
即弦AB所对的圆周角为60°或120°.
故答案为60°或120°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列函数关系式中,y不是x的函数的是( )
| A. | y=-x | B. | |y|=2x | C. | y=|2x| | D. | y=2x2+4 |
8.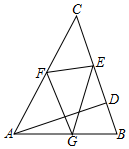 △ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
△ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
 △ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
△ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
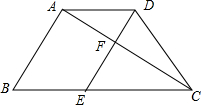 如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求:
如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求: 如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.
如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm. 在平面直角坐标系xOy中,将抛物线y=2x2沿y轴向上平移1个单位,再沿x轴向右平移2个单位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
在平面直角坐标系xOy中,将抛物线y=2x2沿y轴向上平移1个单位,再沿x轴向右平移2个单位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.