题目内容
2.化简求值.(1)(a-3b)(2a+b)+(a+2b)(2b-a),其中a=1,b=-1
(2)y(x+y)+(x+y)(x-y)-x2,其中x=-2,y=$\frac{1}{2}$.
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)先算乘法,再合并同类项,最后代入求出即可.
解答 解:(1)(a-3b)(2a+b)+(a+2b)(2b-a)
=2a2+ab-6ab-3b2+2ab-a2+4b2-2ab
=a2-5ab+b2,
当a=1,b=-1时,原式=12-5×1×(-1)+(-1)2=7;
(2)y(x+y)+(x+y)(x-y)-x2
=y2+xy+x2-y2-x2
=xy,
当x=-2,y=$\frac{1}{2}$时,原式=-2×$\frac{1}{2}$=-1.
点评 本题考查了整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.如果扇形的圆心角为120°,它的面积为12π cm2,那么扇形的半径为( )
| A. | 4cm | B. | 24cm | C. | 12cm | D. | 6cm |
10. 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4m,CA=1m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
17.已知1是关于x的一元二次方程x2+(m-1)x+1=0的一个根,则m的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
14.比较3115和769的大小关系是( )
| A. | 3115>769 | B. | 3115<769 | C. | 3115=769 | D. | 无法判定 |
12.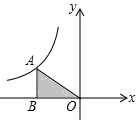 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
 如图,已知四点A,B,C,D,按照下列语句画出图形.
如图,已知四点A,B,C,D,按照下列语句画出图形. △ABC中,∠A=40°,∠B:∠C=1:6,求∠B的度数.
△ABC中,∠A=40°,∠B:∠C=1:6,求∠B的度数.