题目内容
14.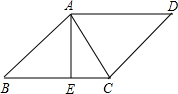 如图,菱形ABCD中,AB=10,cosB=$\frac{3}{5}$,AC⊥BC于点E.求tan∠CAE的值.
如图,菱形ABCD中,AB=10,cosB=$\frac{3}{5}$,AC⊥BC于点E.求tan∠CAE的值.
分析 先由cosB=$\frac{BE}{AB}$=$\frac{3}{5}$求出BE,得出CE,根据勾股定理求出AE,即可求出结果.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=10,
∵AC⊥BC,
在Rt△ABE中,cosB=$\frac{BE}{AB}$=$\frac{3}{5}$,
∴$\frac{BE}{10}=\frac{3}{5}$,
∴BE=6,
∴CE=BC-BE=4,
在Rt△ABE中,$AE=\sqrt{A{B^2}-B{E^2}}=\sqrt{{{10}^2}-{6^2}}=8$,
在Rt△ACE中,tan∠CAE=$\frac{CE}{AE}$=$\frac{4}{8}=\frac{1}{2}$.
点评 本题考查了菱形的性质、解直角三角形的知识;在直角三角形中运用锐角三角函数求出边长是解决问题的关键.

练习册系列答案
相关题目
9.3184900精确到十万位的近似值为( )
| A. | 3.18×106 | B. | 3.19×106 | C. | 3.1×106 | D. | 3.2×106 |
6.已知等腰三角形△ABC中,AB=AC,AD⊥BC于点D,且BC=2AD,则△ABC底角的度数为( )
| A. | 45° | B. | 60° | C. | 75°或15° | D. | 45°或15° |
4. 如图,⊙O中,∠AOC=160°,则∠ABC等于( )
如图,⊙O中,∠AOC=160°,则∠ABC等于( )
 如图,⊙O中,∠AOC=160°,则∠ABC等于( )
如图,⊙O中,∠AOC=160°,则∠ABC等于( )| A. | 20° | B. | 160° | C. | 40° | D. | 80° |
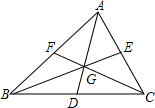 已知:如图,在△ABC中,点D,E,F分别为三边中点,S△BGD=8,那么△ABC的面积是48.
已知:如图,在△ABC中,点D,E,F分别为三边中点,S△BGD=8,那么△ABC的面积是48.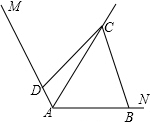 许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.
许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC. 如图在4×4方格中的cosB的值等于$\frac{2\sqrt{5}}{5}$.
如图在4×4方格中的cosB的值等于$\frac{2\sqrt{5}}{5}$.