题目内容
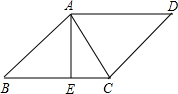
6．已知等腰三角形△ABC中，AB=AC，AD⊥BC于点D，且BC=2AD，则△ABC底角的度数为（ ）| A． | 45° | B． | 60° | C． | 75°或15° | D． | 45°或15° |
分析 根据等腰三角形三线合一的性质可得BD=CD，从而得到AD=BD=CD，再利用等边对等角的性质可得∠B=∠BAD，然后利用直角三角形两锐角互余求解即可．
解答 
解：如图，∵AB=AC，AD⊥BC，
∴BD=CD=$\frac{1}{2}$BC，
∵BC=2AD，
∴AD=BD=CD，
∴∠B=∠BAD=$\frac{1}{2}$（180°-90°）=45°．
故选A．
点评 本题考查了等腰三角形三线合一的性质，等边对等角的性质，得出AD=BD=CD是解题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图，菱形ABCD中，AB=10，cosB=$\frac{3}{5}$，AC⊥BC于点E．求tan∠CAE的值．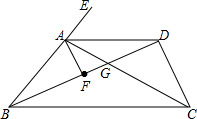
如图，BD平分∠ABC，AF平分∠BAD，∠EAD=2∠DBC，∠BDC=∠AFB，下列结论：①AD∥BC；②∠AFB=90°；③∠FAG=∠DCG，其中正确的是（ ）