题目内容
18. 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧.(1)该圆弧所在的圆心坐标为(2,1);
(2)连结AC,求线段AC和弧AC所围成图形的面积(结果保留π).
分析 (1)根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心.
(2)连接DA、DC、AC,由勾股定理求出AD=DCDA=DC=$\sqrt{10}$,AC=2$\sqrt{5}$,得出DA2+DC2=AC2,由勾股定理的逆定理得出∠ADC=90°,由扇形面积公式和三角形面积公式即可得出结果.
解答 解: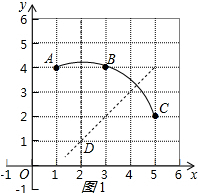 (1)作弦AB和BC的垂直平分线,交点即为圆心,
(1)作弦AB和BC的垂直平分线,交点即为圆心,
如图1所示,圆心D的坐标为(2,1);
故答案为:(2,1);
(2)连接DA、DC,如图2所示:
则DA=DC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴DA2+DC2=AC2,
∴△ADC是等腰直角三角形,∠ADC=90°,
∴线段AC和弧AC所围成图形的面积
=扇形ADC的面积-△DAC的面积
=$\frac{90π×(\sqrt{10})^{2}}{360}$-$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$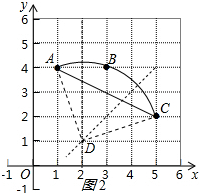
=$\frac{5π}{2}$-5.
点评 本题考查了垂径定理、坐标与图形性质、勾股定理、扇形面积的计算;熟练掌握垂径定理,通过作图求出圆心坐标是解决问题的关键.

练习册系列答案
相关题目
8.下列各式中,从左到右的变形是因式分解的是( )
| A. | 3x+3y-5=3(x+y)-5 | B. | x2+2x+1=(x+1)2 | C. | (x+1)(x-1)=x2-1 | D. | x(x-y)=x2-xy |
13. 如图,△ABC绕点A顺时针旋转95°得到△AEF,若∠BAC=25°,则∠α的度数是( )
如图,△ABC绕点A顺时针旋转95°得到△AEF,若∠BAC=25°,则∠α的度数是( )
 如图,△ABC绕点A顺时针旋转95°得到△AEF,若∠BAC=25°,则∠α的度数是( )
如图,△ABC绕点A顺时针旋转95°得到△AEF,若∠BAC=25°,则∠α的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 70° |
10.下列图形中,具有稳定性的是( )
| A. |  | B. |  | C. |  | D. |  |
7.铁力商厦四楼某商品的标价为1540元,若以9折销售,仍可获利10%(对于进价而言)的利润,则这种商品的进价为( )
| A. | 1260元 | B. | 1386元 | C. | 1000元 | D. | 1200元 |
8.已知y1=-x+5,y2=2x-1
(1)当x取何值时,y1=y2;
(2)当x取何值时,y1的值比y2的值的3倍大1;
(3)先填表,后回答:
根据所填表格,回答问题:随着x的值增大,y1的值逐渐减小;y2的值逐渐增大.
(1)当x取何值时,y1=y2;
(2)当x取何值时,y1的值比y2的值的3倍大1;
(3)先填表,后回答:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y1 | ||||||||
| y2 |
 如图,在Rt△OAA1中,∠OAA1=90°,OA=$\sqrt{3}$,∠AOA1=30°,以OA1为直角边作Rt△OA1A2,∠A1OA2=30°,以OA2为直角边作Rt△OA2A3,∠A2OA3=30°…则OA2016的长度为$\frac{{2}^{2016}\sqrt{3}}{{3}^{1008}}$.
如图,在Rt△OAA1中,∠OAA1=90°,OA=$\sqrt{3}$,∠AOA1=30°,以OA1为直角边作Rt△OA1A2,∠A1OA2=30°,以OA2为直角边作Rt△OA2A3,∠A2OA3=30°…则OA2016的长度为$\frac{{2}^{2016}\sqrt{3}}{{3}^{1008}}$.