题目内容
3.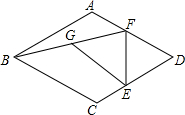 在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.
在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.
分析 作GH⊥EF于H,连接BD,先由菱形的性质得出∠ADO=30°,再由含30°的直角三角形的性质得出GH=$\frac{1}{2}$BM,FH=$\frac{1}{2}$FM,求出OD、BD,再证明△DEF是等边三角形,得出FM=$\frac{5}{3}$,GH=$\frac{11\sqrt{3}}{6}$,HE=$\frac{5}{2}$,然后根据勾股定理求出EG.
解答 解:作GH⊥EF于H,连接BD,如图所示: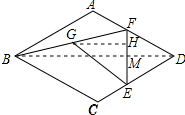 ∵四边形ABCD是菱形,∠BAD=120°,
∵四边形ABCD是菱形,∠BAD=120°,
∴∠ADC=60°,BD平分∠ADC,AC⊥BD,
∴∠ADO=30°,GH∥BD,
∵G为BF的中点,
∴GH=$\frac{1}{2}$BM,FH=$\frac{1}{2}$FM,
∵AD=2+$\frac{10}{3}$=$\frac{16}{3}$,
∴OD=AD•cos30°=$\frac{8}{3}\sqrt{3}$,
∴BD=$\frac{16\sqrt{3}}{3}$,
∵ED=FD,
∴△DEF是等边三角形,
∴EF⊥BD,EF=DF=$\frac{10}{3}$,FM=$\frac{5}{3}$,DM=$\frac{5\sqrt{3}}{3}$,
∴FH=$\frac{5}{6}$,BM=$\frac{11\sqrt{3}}{3}$,
∴GH=$\frac{11\sqrt{3}}{6}$,HE=$\frac{5}{2}$,
∴EG=$\sqrt{(\frac{11\sqrt{3}}{6})^{2}+(\frac{5}{2}})^{2}$=$\frac{7\sqrt{3}}{3}$;
故答案为:$\frac{7\sqrt{3}}{3}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、含30°的直角三角形的性质、三角函数以及勾股定理;本题难度较大,综合性强,需要通过作辅助线才能得出结果.

| A. | 由①式得x=$\frac{7}{3}$+4y,再代入②式 | B. | 由②式得y=$\frac{25+10x}{10}$,再代入①式 | ||
| C. | ①×3得③式,再将③式与②式相减 | D. | 由②式得9x=10y-25,再代入①式 |
| A. | 1.00×10-9 | B. | 9.99×10-8 | C. | 1.002×10-8 | D. | 9.999×10-7 |
| a | 0.000008 | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.02 | 0.2 | 2 | 20 | 200 |
(3)根据你发现的规律填空:
①已知$\root{3}{3}$≈1.442,则$\root{3}{3000}$≈14.42
②已知$\root{3}{0.000456}$≈0.07697,则$\root{3}{456}$≈7.697.
 如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.
如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.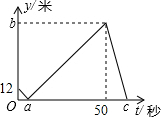 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )