题目内容
11.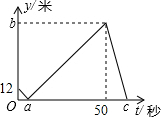 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 易得乙出发时,两人相距12m,除以时间3即为甲的速度;由于出现两人距离为0的情况,那么乙的速度较快.乙50s跑完总路程300可得乙的速度,进而求得50s时两人相距的距离可得b的值,同法求得两人距离为0时,相应的时间,让两人相距的距离除以甲的速度,再加上50即为c的值.
解答 解:甲的速度为:12÷3=4(米/秒);
乙的速度为:300÷50=6(米/秒);
b=6×50-4×(50+3)=88(米);
6a-4×(a+3)=0,
解得a=6,
c=50+88÷4=72(秒),
∴正确的有①②③.
故选:D.
点评 考查一次函数的应用;得到甲乙两人的速度是解决本题的突破点;得到相应行程的关系式是解决本题的关键.

练习册系列答案
相关题目
1.下面的三个图形是由若干个小正方形搭建而成的几何体的三视图,组成几何体的小正方形个数是( )


| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
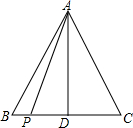 如图,在△ABC中,AB=AC=2,点P在BC上:
如图,在△ABC中,AB=AC=2,点P在BC上: 如图,⊙O的直径CD过弦EF的中点G,且CD=10,EF=8,则tan∠C=$\frac{1}{2}$.
如图,⊙O的直径CD过弦EF的中点G,且CD=10,EF=8,则tan∠C=$\frac{1}{2}$.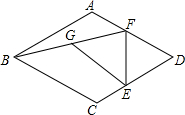 在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.
在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$. 如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为115°.
如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为115°.