题目内容
13.方程组$\left\{\begin{array}{l}{3x-4y=7①}\\{9x-10y+25=0②}\end{array}\right.$的最简便的解法是( )| A. | 由①式得x=$\frac{7}{3}$+4y,再代入②式 | B. | 由②式得y=$\frac{25+10x}{10}$,再代入①式 | ||
| C. | ①×3得③式,再将③式与②式相减 | D. | 由②式得9x=10y-25,再代入①式 |
分析 方程组利用加减消元法解即为简便.
解答 解:方程组$\left\{\begin{array}{l}{3x-4y=7①}\\{9x-10y+25=0②}\end{array}\right.$的最简便的解法是①×3得③式,再将③式与②式相减,
故选C
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
4.下列图形是中心对称而不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.任意买一张电影票,座位号是2的倍数,此事件是( )
| A. | 不可能事件 | B. | 不确定事件 | ||
| C. | 必然事件 | D. | 以上结论都不正确 |
18.在下列各式中,运算结果是m2-$\frac{1}{16}$n4的是( )
| A. | (-$\frac{1}{4}$n2+m)(-$\frac{1}{4}$n2-m) | B. | (m-$\frac{1}{2}$n2)(m-$\frac{1}{8}$n2) | C. | (-$\frac{1}{4}$n2-m)($\frac{1}{4}$n2-m) | D. | (-$\frac{1}{4}$n2+m)($\frac{1}{4}$n2-m) |
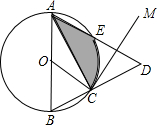 如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.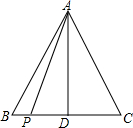 如图,在△ABC中,AB=AC=2,点P在BC上:
如图,在△ABC中,AB=AC=2,点P在BC上: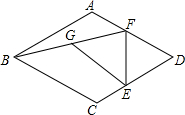 在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.
在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.