题目内容
12.在Rt△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DF∥AB交直线AC于点E.(1)当点D在边BC上时,如图①,求证:DE+DF=$\frac{\sqrt{2}}{2}$BC.
(2)当点D在边BC的延长线上时(如图②)或当点D在边BC的反向延长线上时(如图③),线段DE、DF、BC又有怎样的数量关系?请直接写出你的猜想,并选择其中一种情况加以证明.
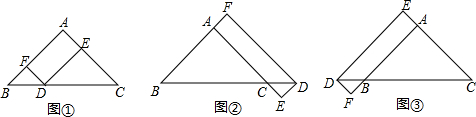
分析 (1)证明四边形AFDE是矩形,且△DEC和△BDF是等腰直角三角形即可证得;
(2)与(1)的证明方法相同;
解答 (1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∵∠A=90°,
∴?AFDE是矩形,
∴∠AFD=∠AED=90°,
∴∠BFD=∠DEF=90°,
∴△BDF和△DEC是等腰直角三角形,
∴BD=$\sqrt{2}DF$,CD=$\sqrt{2}$DE,
∴BC=BD+DC=$\sqrt{2}$(DE+DF),
∴DE+DF=$\frac{\sqrt{2}}{2}$BC;
(2)图②中:DF-DE=$\frac{\sqrt{2}}{2}$BC,
图③中:DE-DF=$\frac{\sqrt{2}}{2}$BC;
证明:如图②,∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∵∠F=∠BAC=90°,
∴?AFDE是矩形,
∴∠AFD=∠AED=90°,
∴△BDF和△DEC是等腰直角三角形,
∴BD=$\sqrt{2}DF$,CD=$\sqrt{2}$DE,
∴BC=BD-DC=$\sqrt{2}$(DF-DE),
∴DF-DE=$\frac{\sqrt{2}}{2}$BC.
点评 本题考查了矩形的判定与性质以及等腰直角三角形的判定和性质,熟记等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
1.下面的三个图形是由若干个小正方形搭建而成的几何体的三视图,组成几何体的小正方形个数是( )


| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
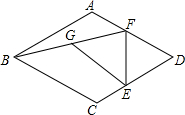 在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$.
在菱形ABCD中,∠BAD=120°,点E,F分别在边CD,AD上,且ED=FD,连接BF,G为BF的中点,连接EG,AF=2,DF=$\frac{10}{3}$,则EG=$\frac{7\sqrt{3}}{3}$. 如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为115°.
如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为115°.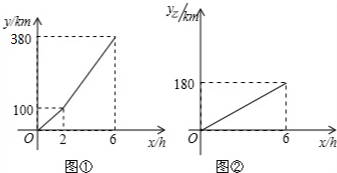
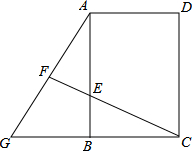 如图,点E在矩形ABCD的边AB上,点G在CB的延长线上,连接AG,直线CE交于AG于点F,若AF=GF,∠BCE=30°,EF=4,AE=8,则BC=4$\sqrt{3}$.
如图,点E在矩形ABCD的边AB上,点G在CB的延长线上,连接AG,直线CE交于AG于点F,若AF=GF,∠BCE=30°,EF=4,AE=8,则BC=4$\sqrt{3}$.