题目内容
12.一元二次方程x(x-4)=-4的根是( )| A. | x=-2 | B. | x=2 | C. | x=2或x=-2 | D. | x=-1或x=2 |
分析 原方程整理成一般式后,利用因式分解法求解可得.
解答 解:原方程整理可得:x2-4x+4=0,
因式分解可得:(x-2)2=0,
则x-2=0,
解得:x=2,
故选:B.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 已知∠1=60°,∠2=120°,∠3=67°,则∠4=( )
已知∠1=60°,∠2=120°,∠3=67°,则∠4=( )
 已知∠1=60°,∠2=120°,∠3=67°,则∠4=( )
已知∠1=60°,∠2=120°,∠3=67°,则∠4=( )| A. | 120° | B. | 125° | C. | 67° | D. | 60° |
17.-2的相反数是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | ±2 | D. | 2 |
1.下列计算正确的是( )
| A. | (-2xy)2=-4x2y2 | B. | x6÷x3=x2 | C. | (x-y)2=x2-y2 | D. | 2x+3x=5x |
8. 如图,在Rt△ABC中,∠C=90°,以三边BC,CA,AB为直径向外作半圆,这些半圆的面积分别为S1,S2,S3,则S1,S2,S3的关系是( )
如图,在Rt△ABC中,∠C=90°,以三边BC,CA,AB为直径向外作半圆,这些半圆的面积分别为S1,S2,S3,则S1,S2,S3的关系是( )
 如图,在Rt△ABC中,∠C=90°,以三边BC,CA,AB为直径向外作半圆,这些半圆的面积分别为S1,S2,S3,则S1,S2,S3的关系是( )
如图,在Rt△ABC中,∠C=90°,以三边BC,CA,AB为直径向外作半圆,这些半圆的面积分别为S1,S2,S3,则S1,S2,S3的关系是( )| A. | S1+S2=S3 | B. | S12+S22=S32 | C. | $\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$=$\sqrt{{S}_{3}}$ | D. | 无法确定 |
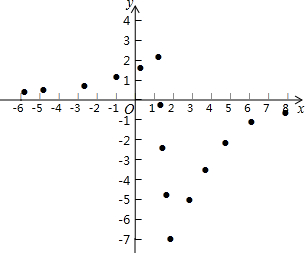 某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整:
某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整: 如图,已知菱形ABCD,AB=5,对角线BD=8,作AE⊥BC于点E,CF⊥AD于点F,连接EF,求EF的长.
如图,已知菱形ABCD,AB=5,对角线BD=8,作AE⊥BC于点E,CF⊥AD于点F,连接EF,求EF的长. 用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为π-$\frac{3}{2}\sqrt{3}$.
用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为π-$\frac{3}{2}\sqrt{3}$.