题目内容
2.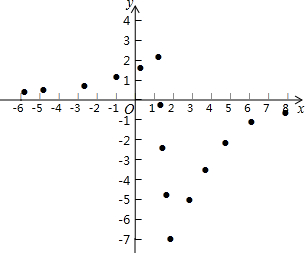 某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整:
某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整:(1)该函数的自变量x的取值范围是x≠2;
(2)结合图象,写出当x<2时,函数在x=1,取得最大值y=2;
(3)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(4)结合画出的函数图象,写出该函数的一条性质:y值随x值的增大而增大.
分析 (1)由分母不为零,可得出自变量x的取值范围;
(2)观察函数图象,可知当x=1时,y取最大值,最大值为2;
(3)连点,画出函数图象;
(4)观察函数图象,写出一条函数的性质即可.
解答 解:(1)∵(x-2)2≠0,
∴x≠2.
故答案为:x≠2.
(2)观察函数图象可知:当x=1时,y取最大值,最大值为2.
故答案为:1;2.
(3)连线,画出函数图象,如图所示.
(4)观察函数图象,当x>0时,y值随x值的增大而增大.
故答案为:y值随x值的增大而增大.
点评 本题考查了二次函数的性质以及二次函数的图象,解题的关键是:(1)由分母不为零,找出自变量x的取值范围;(2)观察函数图象,找出最值;(3)连点,画出函数图象;(4)观察函数图象,找出函数性质.

练习册系列答案
相关题目
17.函数y=3x的图象经过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
14.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N( )
| A. | M=2xy3,N=-15x | B. | M=3xy3,N=-15x2 | C. | M=2xy3,N=-15x2 | D. | M=2xy3,N=15x2 |
11.若x=$\frac{1}{6}$,则$\frac{{x}^{2}+1}{x-6}$•$\frac{{x}^{2}-36}{{x}^{3}+x}$的值( )
| A. | 等于1 | B. | 等于36 | C. | 等于37 | D. | 无意义 |
12.一元二次方程x(x-4)=-4的根是( )
| A. | x=-2 | B. | x=2 | C. | x=2或x=-2 | D. | x=-1或x=2 |
 如图,已知∠1和∠2互余,∠2与∠3互补,∠3=140°,求∠4的度数.
如图,已知∠1和∠2互余,∠2与∠3互补,∠3=140°,求∠4的度数. 如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{k_2}{x}$的图象相交与A,B两点,其横坐标分别为2和6,则不等式k1x<$\frac{k_2}{x}$-b的解集是0<x<2或x>6.
如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{k_2}{x}$的图象相交与A,B两点,其横坐标分别为2和6,则不等式k1x<$\frac{k_2}{x}$-b的解集是0<x<2或x>6. 钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离($\sqrt{2}$≈1.414,结果精确到0.01)
钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离($\sqrt{2}$≈1.414,结果精确到0.01) 某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题:
某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题: