题目内容
19.圆锥体的底面半径为2,全面积为12π,则其侧面展开图的圆心角为( )| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
分析 根据圆锥的侧面积公式S=πrl得出圆锥的母线长,再结合扇形面积公式即可求出圆心角的度数.
解答 解:∵底面半径为2,
∴底面积为4π,
∵全面积为12π,
∴侧面积为8π,
∴圆锥侧面积公式为:S=πrl=π×2×l=8π,
解得:l=4,
∴扇形面积为8π=$\frac{nπ×{4}^{2}}{360}$,
解得:n=180,
∴侧面展开图的圆心角是180度.
故选D.
点评 此题主要考查了圆锥的侧面积公式应用以及与展开图扇形面积关系,求出圆锥的母线长是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.二元一次方程组$\left\{\begin{array}{l}{x+y=5k}\\{x-y=9k}\end{array}\right.$的解是二元一次方程2x+3y=8的解,则k的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
4. 如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )
如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )
 如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )
如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
8.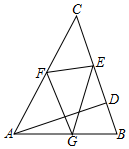 △ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
△ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
 △ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
△ABC中,∠BAC=60°,AD⊥BC于D,且AD=$\sqrt{3}$,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
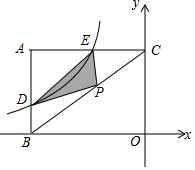 如图,在平面直角坐标系中,矩形OCAB的两边在直角坐标系的坐标轴上,顶点A在第二象限,OB=4,OC=3,点D是边AB上的一个动点(点D不与A,B重合),过点D的反比例函数y=$\frac{m}{x}$的图象与边AC交于点E.
如图,在平面直角坐标系中,矩形OCAB的两边在直角坐标系的坐标轴上,顶点A在第二象限,OB=4,OC=3,点D是边AB上的一个动点(点D不与A,B重合),过点D的反比例函数y=$\frac{m}{x}$的图象与边AC交于点E.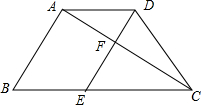 如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求:
如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求: 如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.
如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.