题目内容
如图，E是正方形ABCD申CD边上任意一点．（1）以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形；
（2）在BC边上画一点F，使△CFE的周长等于正方形ABCD的周长的一半，请简要说明你取该点的理由．
考点：作图-旋转变换
专题：
分析：（1）利用旋转的性质得出△ABE′的位置；
（2）根据全等三角形的判定与性质得出△AEF≌△AE′F（SAS），以及EF=E′F=BF+DE，进而得出EF+EC+FC=BC+CD．
（2）根据全等三角形的判定与性质得出△AEF≌△AE′F（SAS），以及EF=E′F=BF+DE，进而得出EF+EC+FC=BC+CD．
解答：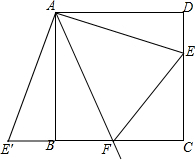
解：（1）如图所示：△ABE′即为所求；
（2）作∠EAE′的平分线交BC于点F，则△CFE的周长等于正方形ABCD的周长的一半，
在△AEF和△AE′F中
∵
，
∴△AEF≌△AE′F（SAS），
∴EF=E′F=BF+DE，
∴EF+EC+FC=BC+CD．
解：（1）如图所示：△ABE′即为所求；（2）作∠EAE′的平分线交BC于点F，则△CFE的周长等于正方形ABCD的周长的一半，
在△AEF和△AE′F中
∵
|
∴△AEF≌△AE′F（SAS），
∴EF=E′F=BF+DE，
∴EF+EC+FC=BC+CD．
点评：此题主要考查了图形的转变换以及全等三角形的判定与性质，得出△AEF≌△AE′F是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，O是正方形ABCD的两条对角线BD，AC的交点，EF过点O，若图中阴影部分的面积为1，则正方形ABCD的周长为
如图，将△ABC绕点O旋转，使顶点A与点A′重合，画出旋转后的图形．
如图，AB=12，C为AB的中点，点D在线段AC上，且AD：CB=1：3，则DB的长度为（ ）| A、4 | B、6 | C、8 | D、10 |
如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，将线段AB绕点B顺时针旋转90°．将线段A′B，点A的对应点为A′，连接AA′交线段BC于点D．