题目内容
两对角线分别是 6cm 和 8cm 的菱形面积是_____cm2.
24 【解析】【解析】 ∵菱形的两条对角线分别是6cm和8cm,∴这个菱形的面积是: ×6×8=24(cm2).故答案为:24.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知二次函数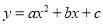 的图像上部分点的坐标
的图像上部分点的坐标 满足下表:
满足下表:
| … |
|
|
|
| … |
| … |
|
|
|
| … |
(1)求这个二次函数的解析式;
(2)用配方法求出这个二次函数图像的顶点坐标和对称轴.
(1)(2)顶点坐标为; 对称轴是直线 【解析】试题分析:(1)运用待定系数法求解即可; (2)运用配方法得y,从而求出顶点坐标和对称轴. 试题解析:(1)由题意,得 解这个方程组,得 , 所以,这个二次函数的解析式是. (2) 顶点坐标为; 对称轴是直线.

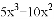 =___________.
=___________.
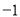
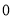
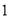
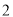
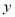
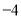
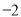
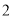
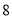
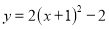 与
与 轴的交点的坐标是( )
轴的交点的坐标是( )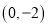 ; B.
; B. 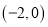 ; C.
; C. 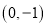 ; D.
; D. 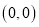 .
.

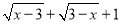 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )