题目内容
12.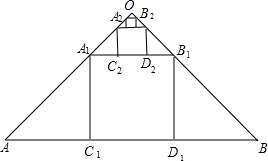 如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第2015个正方形A2015B2015C2015D2015的边长是$(\frac{1}{3})^{2015}$.
如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第2015个正方形A2015B2015C2015D2015的边长是$(\frac{1}{3})^{2015}$.
分析 根据题意可知∠A=45°,∠AC1A1=90°,故此△AC1A1是等腰直角三角形,同理可证明△BD1B1是等腰直角三角形,由A1B1C1D1是正方形可知AC1=C1D1=D1B,从而得到${C}_{1}{D}_{1}=\frac{1}{3}AB$,同理:${C}_{2}{D}_{2}=\frac{1}{3}{A}_{1}{B}_{1}$,依据规律可求得正方形A2015B2015C2015D2015的边长=$(\frac{1}{3})^{2015}$.
解答 解:∵△ABO是等腰直角三角形,
∴∠A=∠B=45°.
∵四边形A1B1C1D1是正方形,
∴∠AC1A1=90°.
∵∠A=45°,∠AC1A1=90°,
∴△AC1A1是等腰直角三角形.
同理△BD1B1是等腰直角三角形.
∴${C}_{1}{D}_{1}=\frac{1}{3}AB$.
同理:${C}_{2}{D}_{2}=\frac{1}{3}{A}_{1}{B}_{1}$,
…
A2015B2015C2015D2015的边长=$(\frac{1}{3})^{2015}$.
故答案为:$(\frac{1}{3})^{2015}$.
点评 本题主要考查的是正方形的性质、等腰直角三角形的性质和判定,证得${C}_{1}{D}_{1}=\frac{1}{3}AB$是解题的关键.

练习册系列答案
相关题目
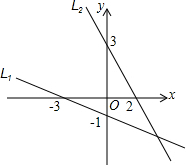 如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解. 如图,在△ABC中,∠ACB=90°,AB=10cm,点D为AB的中点,则CD=5cm.
如图,在△ABC中,∠ACB=90°,AB=10cm,点D为AB的中点,则CD=5cm.