题目内容
19.以A(2,3)为圆心的圆与两坐标轴共有三个公共点,则⊙A的半径是3或$\sqrt{13}$.分析 由A(2,3)得点A到x轴的距离是4,到y轴的距离是3;根据题意分析,知该圆要想与坐标轴共有3个交点,应有两种情况;
解答 解:因为圆心的圆与两坐标轴共有三个公共点,所以圆与x、y轴有2种情况:有一点与x轴相切,此时半径为3;
当圆与原点相交时,此时圆与两坐标轴共有三个公共点,且半径为$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
故⊙A的半径是3或$\sqrt{13}$.
故答案为:3或$\sqrt{13}$.
点评 此题主要考查了直线与圆的位置关系以及坐标与图形的性质,能够正确分析出圆与坐标轴有3个公共点时的位置关..

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
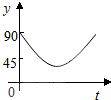
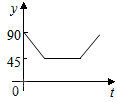
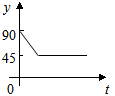
 如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )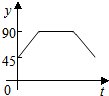
 有理数a,b在数轴上的位置如图所示.
有理数a,b在数轴上的位置如图所示.