题目内容
14.如图,△ABC和△ADE是等腰直角三角形,∠ADE=∠ACB=90°,连接BE,F为BE的中点,连接CF、DF.(1)如图1,当AD与AC重合时,猜想线段CF、DF的关系,并证明你的猜想;
(2)如图2,当DA⊥AB时,(1)中猜想的结论是否成立?请说明理由;
(3)如图3,若△ABC不动,△ADE绕点A旋转任意一个角度,其他条件不变,(1)中的结论成立吗?请直接回答,不必说明理由.

分析 (2)先证明△DEF≌△GCF,得到DE=CG,DF=FG,根据AD=DE,AB=BC,得到BD=BG又因为∠ABC=90°,所以DF=CF且DF⊥BF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,DF=FH,再判断出△DAC≌△HBC,即可得出CD=CH,即可得出结论;
(3)过点B作BH∥ED,与DF的延长线交于点H,连接CH,推出△FDE≌△FHB,求出DF=HF,DE=BH,作AN⊥EB于点N,证△CBH≌△CAD,推出CH=CD,∠DCA=∠BCH,求出∠DCH=90°,即可得出答案.
解答 证明:(1)DF=CF,DF⊥CF
理由:如图1,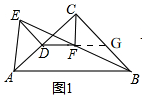
∵∠ADE=∠ACB=90°,
∴DE∥BC,
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE中点,
∴EF=BF.
∴△DEF≌△GBF.
∴DE=GB,DF=GF.
∵AD=DE,
∴AD=GB,
∵AC=BC,
∴AC-AD=BC-GB,
∴DC=GC.
∵∠ACB=90°,
∴△DCG是等腰直角三角形,
∵DF=GF.
∴DF=CF,DF⊥CF.
(2)如图2,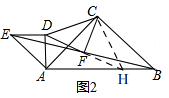
延长DF交BA于点H,
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠DAE=∠ABC=45°,
∵CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,
∴△DEF≌△HBF,
∴DF=HF,ED=HB,
∵AD=ED,
∴AD=HB
在△ADC和△BHC中,$\left\{\begin{array}{l}{AD=HB}\\{∠DAC=∠HBC=45°}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△BHC,
∴DC=HC,
∴△DCH是等腰直角三角形,
∵DF=HF,
∴DF=CF,DF⊥CF;
(3)DF=CF,DF⊥CF;
理由:如图3,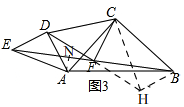
过点B作BH∥ED,与DF的延长线交于点H,连接CH,
∴∠DEF=∠BHF,
在△FDE和△FHB中,$\left\{\begin{array}{l}{∠DEF=∠BHF}\\{EF=BF}\\{∠DFE=∠HFB}\end{array}\right.$,
∴△FDE≌△FHB,
∴DF=FH,DE=HB,
∴AD=ED=HB,
作AN⊥EB于点N,
由已知∠ADE=90°,∠ACB=90°,
可证得∠DEN=∠DAN,∠NAC=∠CBF,
∵BH∥ED,
∴∠DEN=∠HBF,
∴∠CBH=∠CBF+∠HBF=∠NAC+∠DEN=∠NAC+∠DAN=∠CAD,
在△CBH和△CAD中,$\left\{\begin{array}{l}{BC=AC}\\{∠CBH=∠CAD}\\{BH=AD}\end{array}\right.$,
∴△CBH≌△CAD,
∴CH=CD,∠DCA=∠BCH,
∴∠DCH=∠DCA+∠ACH=∠BCH+∠ACH=∠ACB=90°,
∵DF=HF,
∴DF=CF,DF⊥CF.
点评 此题是几何变换综合题,主要考查了旋转的性质,等腰三角形和全等三角形的判定,及勾股定理的运用.要掌握等腰三角形和全等三角形的性质及其判定定理并会灵活应用是解题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:
已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:①b2>4ac;②abc>0;③(a+c)2>b2;④3a+c>0,
其中,正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
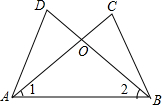 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |


 利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1).
利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1). 如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长.
如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长.