题目内容
5．
如图，AD是△ABC的高，点E在AC上，且EG⊥BC于G，∠1=∠2，∠3=58°，∠C=35°，求∠BAC的度数．
分析 根据平行线的判定推出AD∥EG，根据平行线的性质得出∠2=∠DAB，求出∠1=∠DAB，根据平行线的判定得出DF∥AB，根据平行线的性质得出∠3=∠B=58°，根据三角形的内角和定理求出即可．
解答 解：∵AD是△ABC的高，BE⊥BC，
∴∠ADB=∠EGB=90°，
∴AD∥EG，
∴∠2=∠DAB，
∵∠1=∠2，
∴∠1=∠DAB，
∴DF∥AB，
∴∠3=∠B=58°，
∵∠C=35°，
∴∠BAC=180°-∠B-∠C=87°．
点评 本题考查了平行线的性质和判定，三角形的内角和定理的应用，能推出DF∥AB是解此题的关键，难度适中．
练习册系列答案
相关题目
16．以O（2，2）为圆心，3为半径作圆，则⊙O与直线y=kx+$\frac{1}{5}$k的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 都有可能 |
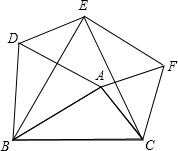（1）感知：如图，分别以△ABC的三边为边长，在BC边的同侧分别作三个等边三角形，即△ABD，△BCE，△ACF，连接DE、EF，试猜想四边形ADEF的形状，并证明你的猜想．
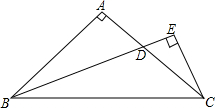如图，Rt△ABC中，AB=AC，∠A=90°，∠B的平分线交AC于D，从C点向BD的延长线作垂线，垂足为E．求证：BD=2CE．
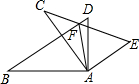已知，如图，AB⊥AD，AC⊥AE，AB=AC，AD=AE．求证：