题目内容
1.化简:($\frac{1}{2}$x-y)2-$\frac{1}{4}$(x+y)(x-y)分析 首先利用完全平方公式和平方差公式计算,然后去括号、合并同类项即可.
解答 解:原式=$(\frac{1}{2}x-y)^{2}-\frac{1}{4}({x}^{2}-{y}^{2})$
=$\frac{1}{4}{x}^{2}-xy+{y}^{2}-\frac{1}{4}{x}^{2}+\frac{1}{4}{y}^{2}$
=$\frac{5}{4}{y}^{2}-xy$.
点评 本题主要考查的是平方差公式和完全平方公式的应用,掌握公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.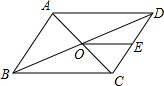 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )| A. | 24 | B. | 15 | C. | 21 | D. | 30 |
16.以O(2,2)为圆心,3为半径作圆,则⊙O与直线y=kx+$\frac{1}{5}$k的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 都有可能 |
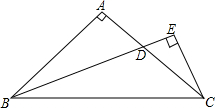 如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE.
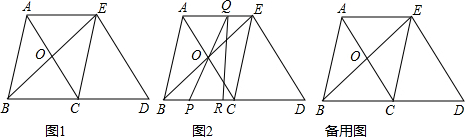
如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE. 已知AD是BC边上的中线,AF=2FD,求证:AE=EC.
已知AD是BC边上的中线,AF=2FD,求证:AE=EC.