题目内容
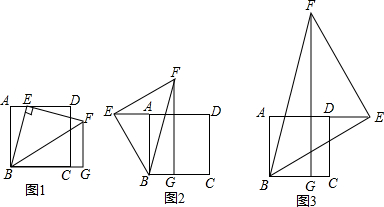
2.小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF.(S表示面积)
问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,而此时P点正好是线段MN的中点,你能想明白其中的道理吗,请认真理解,然后运用结论解决下面问题.
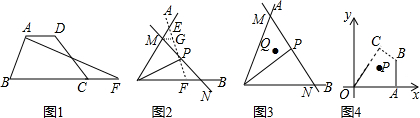
(1)如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66°≈0.91,tan66°≈2.25,$\sqrt{3}$≈1.73)
(2)如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)(6,3)($\frac{9}{2}$,$\frac{9}{2}$)、(4、2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,请直接写出以点O为顶点的四边形面积的最大值是10.
分析 (1)根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论;
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论;
(2)分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
(3)当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较就可以求出结论.
解答 解:问题情境:证明:∵AD∥BC,∴∠ADE=∠FCE,在△ADE与△FCE中,$\left\{\begin{array}{l}{∠ADE=FCE}\\{DE=CE}\\{∠AED=∠FEC}\end{array}\right.$,
∴△ADE≌△FCE,∴S△ADE=S△FCE,
∴S四边形ABCD=S四边形ABCE+S△ADE=S四边形ABCE+S△FCE=S△ABF;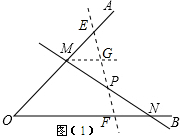 解:(1)当直线旋转到点P是MN的中点时S△MON最小,
解:(1)当直线旋转到点P是MN的中点时S△MON最小,
如图(1),过点P的另一条直线EF交OA、OB于点E、F,设PF<PE,过点M作MG∥OB交EF于G,
由方法探究可以得出当P是MN的中点时S四边形MOFG=S△MON.
∵S四边形MOFG<S△EOF,
∴S△MON<S△EOF,
∴当点P是MN的中点时S△MON最小;
(2)实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,
在Rt△OPP1中,∠POB=30°,
∴PP1=$\frac{1}{2}$,OP=2km,OP1=OP cos∠POB=2km,
由方法探究的结论知道,当PM=PN时,△MON的面积最小,
∵PP1∥MM1
∴△N PP1∽△NMM1
∴MM1=2PP1=4 km,M1P1=P1N,
在Rt△OMM1中,∠AOB=70°,
∴OM1=$\frac{M{M}_{1}}{tan∠AOB}$=$\frac{4}{tan66°}$ km,
∴M1P1=P1N=(2-$\frac{4}{tan66°}$) km,
∴ON=OP1+P1N=2+(2-$\frac{4}{tan66°}$)=(4-$\frac{4}{tan66°}$) km,
∴S△MON=$\frac{1}{2}$ON•MM1=$\frac{1}{2}$ (4-$\frac{4}{tan66°}$)×4≈3.6km2.
(3)拓展延伸:①如图4,当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,
∵C($\frac{9}{2}$,$\frac{9}{2}$),
∴∠AOC=45°,
∴AO=AD.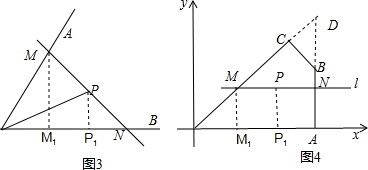
∵A(6,0),
∴OA=6,
∴AD=6.
∴S△AOD=$\frac{1}{2}$×6×6=18,
由问题迁移的结论可知,当PN=PM时,△MND的面积最小,
∴四边形ANMO的面积最大.
作PP1⊥OA,MM1⊥OA,垂足分别为P1,M1,
∴M1P1=P1A=2,
∴OM1=M1M=2,
∴MN∥OA,
∴S四边形OANM=S△OMM1+S四边形ANMM1=$\frac{1}{2}$×2×2+2×4=10
②如图5,当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,
∵C($\frac{9}{2}$,$\frac{9}{2}$)、B(6,3),设直线BC的解析式为y=kx+b,由题意,得$\left\{\begin{array}{l}{\frac{9}{2}=\frac{9}{2}k+b}\\{3=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=9}\end{array}\right.$,
∴y=-x+9,
当y=0时,x=9,
∴T(9,0).
∴S△OCT=$\frac{1}{2}$×$\frac{9}{2}$×9=$\frac{81}{4}$,
由问题迁移的结论可知,当PM=PN时,△MNT的面积最小,
∴四边形CMNO的面积最大.
∴NP1=M1P1,MM1=2PP1=4,
∴4=-x+9,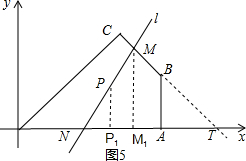
∴x=5,
∴M(5,4),
∴OM1=5,
∵P(4,2),
∴OP1=4,
∴P1M1=NP1=1,
∴ON=3,
∴NT=6,
∴S△MNT=$\frac{1}{2}$×4×6=12,
∴S四边形OCMN=$\frac{81}{4}$-12=$\frac{33}{4}$<10.
∴综上所述:截得四边形面积的最大值为10.
故答案为:10.
点评 本题考查了由特殊到一般的数学思想的运用,全等三角形的判定及性质的运用,勾股定理的运用,待定系数法求一次函数的解析式的运用,四边形的面积公式的运用,三角形的面积公式的运用,分类讨论思想的运用,解答时建立数学模型解答是关键.

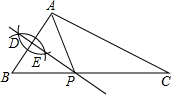 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )| A. | PA+PC=BC | B. | PA=PB | C. | DE⊥AB | D. | PA=PC |
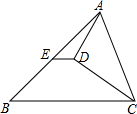 如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
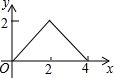
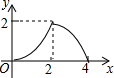
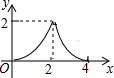
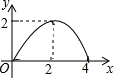
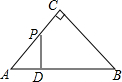 如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )