题目内容
20. 如图,∠C=90°,AC=3,BC=4,AD=12,BD=13.
如图,∠C=90°,AC=3,BC=4,AD=12,BD=13.(1)试判断△ABD的形状,并说明理由;
(2)求出四边形ACBD的面积.
分析 (1)先由勾股定理求出AB,再由勾股定理的逆定理即可得出△ABD是直角三角形;
(2)四边形ACBD的面积=△ABC的面积+△ABD的面积=$\frac{1}{2}$AC•BC+$\frac{1}{2}$AB•AD,即可得出结果.
解答 解:(1)△ABD是直角三角形;理由如下:
∵∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵52+122=132,
∴AB2+AD2=BD2,
∴△ABD是直角三角形,∠BAD=90°;
(2)四边形ACBD的面积=△ABC的面积+△ABD的面积
=$\frac{1}{2}$AC•BC+$\frac{1}{2}$AB•AD
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12
=36.
点评 本题考查了勾股定理、勾股定理的逆定理、直角三角形面积的计算方法;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )| A. | 12件 | B. | 8.625件 | C. | 8.5件 | D. | 9件 |
5.下列函数中,y是x的反比例函数的是( )
| A. | y=x-1 | B. | y=$\frac{8}{{x}^{2}}$ | C. | $\frac{y}{x}$=2 | D. | y=$\frac{1}{2x}$ |

 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.
如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.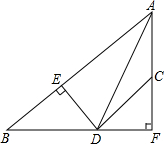 如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.
如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD. 如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 300m,结果他在水中实际游了500m,求该河流的宽度为400m.
如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 300m,结果他在水中实际游了500m,求该河流的宽度为400m. 如图.抛物线y=$\frac{1}{2}$x2-2交x轴于A、B两点.
如图.抛物线y=$\frac{1}{2}$x2-2交x轴于A、B两点.