题目内容
抛物线y=x2-3x+2的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:二次函数的性质
专题:
分析:先利用配方法求出顶点坐标,再根据各象限内点的坐标特点进行解答.
解答:解:∵y=x2-3x+2=(x-
)2-
+2=(x-
)2-
,
∴顶点坐标为(
,-
),
∴顶点在第四象限.
故选D.
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
∴顶点坐标为(
| 3 |
| 2 |
| 1 |
| 4 |
∴顶点在第四象限.
故选D.
点评:本题考查的是二次函数的性质及各象限内点的坐标特点,根据题意得出抛物线的顶点坐标是解答此题的关键.

练习册系列答案
相关题目
形如x2+bx-c=0或形如x2-bx-c=0的方程,如果其中的b,c为1,2,3,…,9中的一个正整数,且方程至少有一根也为1,2,3,…,9中的一个正整数,就称该方程为“漂亮方程”,则“漂亮方程”的个数为( )
| A、20 | B、22 | C、24 | D、26 |
 如图,P是正方形ABCD对角线AC上一点,若PC=AB,则∠PBD等于( )
如图,P是正方形ABCD对角线AC上一点,若PC=AB,则∠PBD等于( )| A、22° | B、22.5° |
| C、25.5° | D、30° |
 如图,AB、CD为⊙O的直径,
如图,AB、CD为⊙O的直径,
 如图,射线CD的端点C在直线AB上,按照下面的要求画图,并标出相应的字母,过点P画直线PE,交AB于点E,过点P画射线PF交射线CD于点F,画线段EF,PC,两条线段交于点F.
如图,射线CD的端点C在直线AB上,按照下面的要求画图,并标出相应的字母,过点P画直线PE,交AB于点E,过点P画射线PF交射线CD于点F,画线段EF,PC,两条线段交于点F.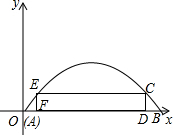 如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.
如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.