题目内容
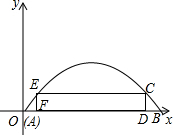 如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.
如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.(1)求抛物线形大门的高度y m与水平距离x m的函数解析式;
(2)求宣传条幅CE至少需要多少?
考点:二次函数的应用
专题:
分析:(1)根据题意将顶点坐标和B点的坐标即可利用待定系数法确定二次函数的解析式;
(2)代入y=1.7求得点E和点C的横坐标,差即为条幅的宽度.
(2)代入y=1.7求得点E和点C的横坐标,差即为条幅的宽度.
解答:解:(1)由图象知:抛物线过原点,
则设抛物线的解析式为y=ax2+bx,
由题意得:顶点坐标为(9.8.1),B(18,0),
故
,
解得:
,
故抛物线形大门的高度y m与水平距离x m的函数解析式为y=-
x2+
x;
(2)令y=-
x2+
x=1.7,
x2-36+51=0,
解得:x1=18+
,x2=18-
,
x1-x2=18+
-(18-
)=2
(m),
答:宣传条幅CE至少需要2
m.
则设抛物线的解析式为y=ax2+bx,
由题意得:顶点坐标为(9.8.1),B(18,0),
故
|
解得:
|
故抛物线形大门的高度y m与水平距离x m的函数解析式为y=-
| 1 |
| 30 |
| 6 |
| 5 |
(2)令y=-
| 1 |
| 30 |
| 6 |
| 5 |
x2-36+51=0,
解得:x1=18+
| 373 |
| 373 |
x1-x2=18+
| 373 |
| 373 |
| 373 |
答:宣传条幅CE至少需要2
| 373 |
点评:本题考查了二次函数的应用,利用了待定系数法求解析式,求相应自变量的值.

练习册系列答案
相关题目
抛物线y=x2-3x+2的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
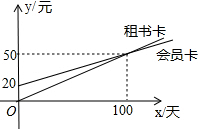 某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示:
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示: 如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD=
如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD=