题目内容
20.一个多边形的内角和是1080°,则这个多边形是八边形,如果这个多边形的每一个外角都相等,则每个外角为45度.分析 设这个多边形的边数为n,根据多边形的内角和定理得到(n-2)×180°=1080°,然后解方程得到这个多边形是几边形,再用360°除以边数即可求解.
解答 解:设这个多边形的边数为n,则
(n-2)×180°=1080°,
解得n=8,
360°÷8=45°.
故这个多边形为八边形,每个外角为45度,.
故答案为:八,45.
点评 本题考查了多边形的内角和定理:n边形的内角和为(n-2)×180°.以及多边形的外角和等于360度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
5.已知MN是⊙O的一条非直径的弦,则下列说法中错误的是( )
| A. | M、N两点到圆心O的距离相等 | |
| B. | MN是圆的一条对称轴 | |
| C. | 在圆中可画无数条与MN相等的弦 | |
| D. | 圆上有两条弧,一条是优弧,一条是劣弧 |
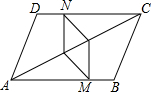 如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形.
如图,在?ABCD中,CN=AM,AE=CF,求证:四边形MENF是平行四边形. 如图所示,在△ABC中,AD⊥BC,D为垂足,AE是△ABC中∠BAC的平分线,∠B=45°,∠AED=80°,求∠C,∠EAD的度数.
如图所示,在△ABC中,AD⊥BC,D为垂足,AE是△ABC中∠BAC的平分线,∠B=45°,∠AED=80°,求∠C,∠EAD的度数.