题目内容
6.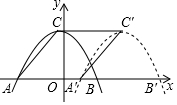 如图,抛物线的顶点为C(-1,8),交x轴于A(-7,0)与点B.将此抛物线向右平移使得A,B,C分别移至A',B',C',若四边形CAA'C'为菱形,则点B′的坐标为( )
如图,抛物线的顶点为C(-1,8),交x轴于A(-7,0)与点B.将此抛物线向右平移使得A,B,C分别移至A',B',C',若四边形CAA'C'为菱形,则点B′的坐标为( )| A. | (5,0) | B. | (13,0) | C. | (15,0) | D. | (17,0) |
分析 首先求出B点坐标,由题意AC=AA′=BB′=10,由此即可解决问题.
解答 解:∵抛物线的顶点为C(-1,8),交x轴于A(-7,0)与点B,
∴B(5,0),AC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵四边形CAA'C'为菱形,
∴AC=AA′=10,
∴AA′=BB′=10,
∴B′(15,0).
故选C.
点评 本题考查抛物线与x轴的交点,二次函数与几何变换,菱形的性质等知识,解题的关键是灵活运用所学知识,理解AA′=BB′是解题的突破点,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.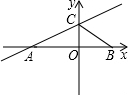 如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
 如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )
如图,直线y=$\frac{1}{3}$x+1与x轴,y轴分别相交于点A,C两点,点B在x轴上,连结BC,若∠ACB=135°,则点B的坐标为( )| A. | (1,0) | B. | ($\sqrt{2}$,0) | C. | (2,0) | D. | ($\sqrt{5}$,0) |
17. 有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论正确的是( )| A. | a+b<0 | B. | a+b>0 | C. | a-b>0 | D. | b-a=0 |
14.甲、乙两个搬运工搬运某种货物,已知乙比甲每小时多搬运600kg,甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等,求甲、乙两人每小时分别搬运多少kg货物.设甲每小时搬运xkg货物,则可列方程为( )
| A. | $\frac{5000}{x-600}$=$\frac{8000}{x}$ | B. | $\frac{5000}{x+600}$=$\frac{8000}{x}$ | C. | $\frac{5000}{x}$=$\frac{8000}{x+600}$ | D. | $\frac{5000}{x}$=$\frac{8000}{x-600}$ |
1.下列关于单项式-$\frac{3x{y}^{2}}{5}$的说法中,正确的是( )
| A. | 系数是-$\frac{3}{5}$,次数是2 | B. | 系数是$\frac{3}{5}$,次数是2 | ||
| C. | 系数是-$\frac{3}{5}$,次数是3 | D. | 系数是-3,次数是3 |
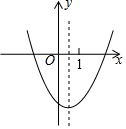 二次函数y=ax2+bx+c的图象如图所示,下列说法正确的个数为( )
二次函数y=ax2+bx+c的图象如图所示,下列说法正确的个数为( )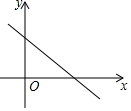 如图,已知一次函数y=-x+4与反比例函数y=$\frac{k}{x}$(k为常数,k≠0).
如图,已知一次函数y=-x+4与反比例函数y=$\frac{k}{x}$(k为常数,k≠0).