题目内容
3.(1)计算:$\sqrt{12}$-|-5|+3tan30°-($\frac{1}{2016}$)0(2)解方程:$\frac{x-1}{x}$+$\frac{3}{x+1}$=1.
分析 (1)原式利用二次根式性质,绝对值的代数意义,特殊角的三角函数值,以及零指数幂法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2$\sqrt{3}$-5+$\sqrt{3}$-1=3$\sqrt{3}$-6;
(2)去分母得:x2-1+3x=x2+x,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解.
点评 此题考查了解分式方程,以及实数的运算,解分式方程注意要检验.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
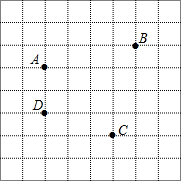 如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.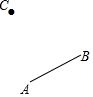 已知AB是⊙O的弦,点C为圆上一点.
已知AB是⊙O的弦,点C为圆上一点.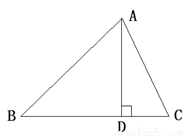
 与容器内水深
与容器内水深 间的函数关系的图象可能是( )
间的函数关系的图象可能是( )
 B.
B.  C.
C.  D.
D. 