题目内容
11.已知$\frac{1}{a}$-$\frac{1}{b}$=$\sqrt{3}$,则$\frac{a}{b(a-b)}$-$\frac{2a-b}{a(a-b)}$的值为-$\sqrt{3}$.分析 原式通分并利用同分母分式的减法法则变形,将已知等式化简后代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-2ab+{b}^{2}}{ab(a-b)}$=$\frac{(a-b)^{2}}{ab(a-b)}$=$\frac{a-b}{ab}$,
由$\frac{1}{a}$-$\frac{1}{b}$=-$\frac{a-b}{ab}$=$\sqrt{3}$,得到a-b=-$\sqrt{3}$ab,
则原式=-$\sqrt{3}$,
故答案为:-$\sqrt{3}$
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.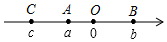 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a-c=b;④$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=1.其中正确的个数有( )
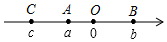 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;②a(b+c)>0;③a-c=b;④$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=1.其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.如图,直线AB,CD相交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=35°,则∠DOT=( )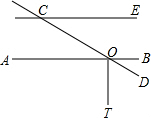

| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
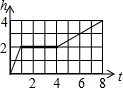
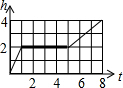
 两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )
两个圆柱形薄玻璃杯(杯身、杯底厚度不计),大杯直径是小杯直径的2倍,把小杯放入大杯中组合成一个容器,其主视图如图所示,现往小杯口中匀速注水,注水过程中杯子始终竖直放置,则下列能反映该容器最高水位h与注水时间t之间关系的大致图象是( )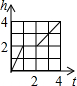

 如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:
如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中: (x>0)的图象如图所示,则以下四个结论:① 两函数图象的交点A的坐标为(3 , 3 ) ;② 当 x>3时 ,y2>yl;③ 当 x =1时, BC = 8;④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是________.
(x>0)的图象如图所示,则以下四个结论:① 两函数图象的交点A的坐标为(3 , 3 ) ;② 当 x>3时 ,y2>yl;③ 当 x =1时, BC = 8;④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是________.