题目内容
14.若2×8n×16n=225,则n的值是3$\frac{3}{7}$.分析 首先根据幂的乘方的运算方法,可得8n=(23)n=23n,16n=(24)n=24n,然后根据2×8n×16n=225,可得21+3n+4n=225,据此求出n的值是多少即可.
解答 解:∵2×8n×16n=225,
∴2×23n×24n=225,
∴21+3n+4n=225,
∴21+7n=225,
∴1+7n=25,
解得n=3$\frac{3}{7}$,
∴n的值是3$\frac{3}{7}$.
故答案为:3$\frac{3}{7}$.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
相关题目
4.下列各式中,去括号正确的是( )
| A. | -(-2x+3)=2x-3 | B. | -(2x-3)=2x+3 | C. | -(-2x-3)=-2x+3 | D. | -(2x+3)=-2x+3 |
2.某水果种植户收获的水果,从上市到销售完需20天,售价为15元/千克,在第x天销售的相关信息如表所示:
(1)写出第x天每销售1kg水果获得的利润?
(2)设该种植户每天获得的利润为y(元),求y关于x的函数关系式,指出第几天获得的利润最大,最大值是多少?
(3)该种植户决定,每销售1kg水果就捐出m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
| 成本P(元/kg) | 8-$\frac{x}{10}$ |
| 销售量q(kg) | 1000-10x |
(2)设该种植户每天获得的利润为y(元),求y关于x的函数关系式,指出第几天获得的利润最大,最大值是多少?
(3)该种植户决定,每销售1kg水果就捐出m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
19.若x=3是方程x2-5mx+6m=0的一个根,则m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
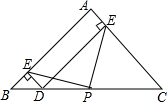 如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.