题目内容
6.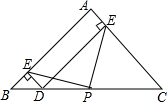 如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
分析 由△ABC是等腰直角三角形得出∠B=45°,AB=AC,求出∠BDF=45°,得出BF=DF,证得四边形AEDF为矩形,连接AP,由等腰三角形三线合一与直角三角形斜边上中线的性质得出AP⊥BC,∠PAC=45°,AP=$\frac{1}{2}$BC=BP,由SAS证得△BPF≌△APE,得出PE=PF,∠APE=∠BPF,证得△EPF为等腰直角三角形,求出EF的长,即可得出结果.
解答 解:∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠B=45°,AB=AC,
∵DF⊥AB,
∴∠BDF=45°,
∴BF=DF,
∵DE⊥AC,
∴四边形AEDF为矩形,
∴AE=DF=BE=$\sqrt{2}$,
连接AP、EF,如图所示: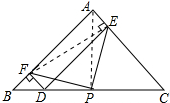
∵P为BC中点,
∴AP⊥BC,∠PAC=45°,AP=$\frac{1}{2}$BC=BP,
在△BPF和△APE中,$\left\{\begin{array}{l}{AE=BF}\\{∠PAE=∠PBE=45°}\\{AP=BP}\end{array}\right.$,
∴△BPF≌△APE(SAS),
∴PE=PF,∠APE=∠BPF,
∴∠EPF=90°,
∴△EPF为等腰直角三角形,
∵BC=8,
∴AB=4$\sqrt{2}$,
∴AF=3$\sqrt{2}$,
EF=$\sqrt{A{F}^{2}+A{E}^{2}}$=$\sqrt{18+2}$=2$\sqrt{5}$,
∴PE=$\sqrt{10}$,
故答案为$\sqrt{10}$.
点评 本题主要考查的是矩形的性质和判定、全等三角形的判定与性质、直角三角形斜边上中线的性质、勾股定理、等腰直角三角形的性质等知识;熟练掌握勾股定理与等腰直角三角形的性质是解决问题的关键.

练习册系列答案
相关题目
16.在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a-b|=44,且AO=3BO,则a+b的值为( )
| A. | -44 | B. | -22 | C. | -55 | D. | -11 |
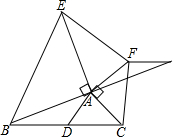 如图,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°.判断线段AD与EF数量和位置关系.
如图,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°.判断线段AD与EF数量和位置关系.