题目内容
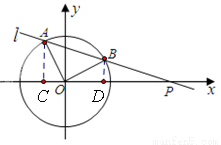
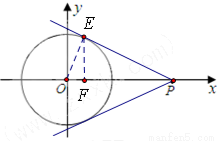
如图,已知平面直角坐标系中,⊙O的圆心在坐标原点,直线l与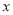 轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程x2-x-k=0 的两根,且两根之差为3.
轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程x2-x-k=0 的两根,且两根之差为3.
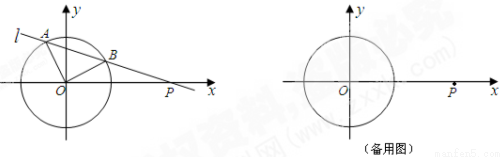
(1)求方程x2-x-k=0 的两根;
(2)求A、B两点的坐标及⊙O的半径;
(3)把直线l绕点P旋转,使直线l与⊙O相切,求直线l的解析式.
(1)2和-1 (2)A(-1,2),B(2,1) 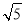 (3)
(3)
【解析】
试题分析:(1)设方程的两根分别为x1,x2(x1>x2),由根与系数的关系可得x1+x2=1,由两根之差为3,可点x1-x2=3,解方程组即可得方程的根;
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,通过△AOC≌△OBD得到A点坐标,利用勾股定理得OA的长;
由A、B在坐标利用待定系数法求出直线AB的解析式,从而得到点P的坐标,过点P的直线与圆相切,有两种情况,因此分切点在第一象限与第四象限两种情况求切线的解析式.
试题解析:(1)设方程的两根分别为x1,x2(x1>x2),由已知得 ,解得
,解得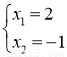 ,∴方程的两根分别为2和-1;
,∴方程的两根分别为2和-1;
(2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,易证:△AOC≌△OBD,∴BD=OC=1,AC=OD=2
∴A(-1,2),B(2,1) ,∴OA=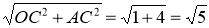
(3)设直线AB的解析式为y=k1x+b1,则 ,解得
,解得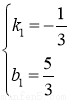 ,∴y=
,∴y=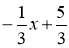 ,当y=0时,
,当y=0时,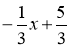 =0,解得x=5,∴P(5,0);
=0,解得x=5,∴P(5,0);
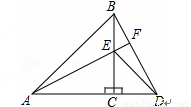
当直线l与⊙O的切点在第一象限时,设直线l与⊙O相切于点E,过点E作EF⊥x轴于点F,∵PE是⊙O的切线,∴OE⊥PE,∴PE= ,∵S△POE=
,∵S△POE=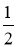 OP·EF=
OP·EF=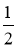 OE·PE,∴5EF=
OE·PE,∴5EF=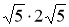 ,∴EF=2,∴OF=
,∴EF=2,∴OF=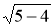 =1,E(1,2);
=1,E(1,2);
设直线l的解析式为y=k2x+b2,则 ,解得
,解得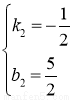 ,∴y= -
,∴y= -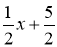 ;
;
当直线l与⊙O的切点在第四象限时,同理可求得y= .
.
考点:1、根与系数的关系;2、三角形全等的判定与性质;3、待定系数法;4、圆的切线.

 B.
B.  C.
C.  D.
D. 
 分别是△
分别是△ 的边
的边 和
和 上的点,
上的点, ,
, ,要使
,要使 ∥
∥ ,
, 应等于 ;
应等于 ;
 中,
中, ,
, ,那么边
,那么边 的长等于( )
的长等于( ) ; B.
; B.  ; C.
; C.  ; D.
; D.  ;
;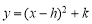 的形式.
的形式. 的一元二次方程
的一元二次方程 有实数根,则k的取值范围是 .
有实数根,则k的取值范围是 . 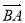 =
=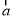 ,
,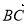 =
=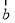 ,试用
,试用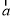 、
、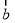 分别表示向量
分别表示向量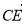 和
和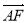 .
. 
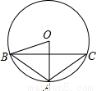
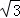 B. 3 C. 2
B. 3 C. 2