题目内容
如 图,△ACB和△E CD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
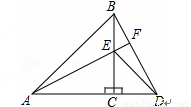
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
(1)证明见解析;(2)垂直,理由见解析.
【解析】
试题分析:(1)根据SAS判定△ACE≌△BCD,从而得到∠EAC=∠DBC,根据角之间的关系可证得AF⊥BD.
(2)互相垂直,只要证明∠AFD=90°,从而转化为证明∠EAC+∠CDB=90即可.
试题解析:(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD,

∴△ACE≌△BCD(SAS);
(2)【解析】
直线AE与BD互相垂直,理由为:
证明:∵△ACE≌△BCD,
∴∠EAC=∠DBC,
又∵∠DBC+∠CDB=90°,
∴∠EAC+∠CDB=90°,
∴∠AFD=90°,
∴AF⊥BD,
即直线AE与BD互相垂直.
考点:1.勾股定理的逆定理;2.直角三角形全等的判定.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目

 ,求AB的长.
,求AB的长.
 ∶1 C、3∶1 D、4∶1
∶1 C、3∶1 D、4∶1 ,则AB的长为 .
,则AB的长为 .
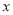 轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程x2-x-k=0 的两根,且两根之差为3.
轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程x2-x-k=0 的两根,且两根之差为3.