题目内容
19.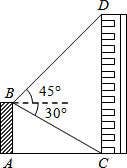 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7).
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7).
分析 首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答 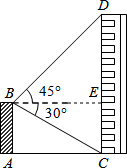 解:如图,过点B作BE⊥CD于点E,
解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=$\frac{BE}{CE}$,
∴BE=CE•cot30°=12×$\sqrt{3}$=12$\sqrt{3}$.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12$\sqrt{3}$.
∴CD=CE+DE=12($\sqrt{3}$+1)≈32.4.
答:楼房CD的高度约为32.4m.
点评 考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.直线y=2x-4与y轴的交点坐标是( )
| A. | (4,0) | B. | (0,4) | C. | (-4,0) | D. | (0,-4) |
10.下列实数中,为无理数的是( )
| A. | 0.2 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | -5 |
7. 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=60,b=0.15;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 20 | 0.10 |
| 70≤x<80 | 30 | b |
| 80≤x<90 | a | 0.30 |
| 90≤x≤100 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
14.我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
4.下列事件是必然事件的是( )
| A. | 地球绕着太阳转 | B. | 抛一枚硬币,正面朝上 | ||
| C. | 明天会下雨 | D. | 打开电视,正在播放新闻 |
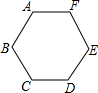 如图,一个零件的横截面是六边形,这个六边形的内角和为720°.
如图,一个零件的横截面是六边形,这个六边形的内角和为720°.