题目内容
14.若$\sqrt{x-2}$+$\sqrt{2-x}$=(x+y)2,则xy=-4.分析 根据二次根式的性质被开方数大于或等于0,即可求得x的值,代入式子即可求得y的值,进而求得xy的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,解得:x=2,
则(2+y)2=0
解得:y=-2,
则xy=-4.
故答案是:-4.
点评 本题主要考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.求得x的值是关键.

练习册系列答案
相关题目
20.计算(-1)×3的结果是( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
9.要使式子$\frac{\sqrt{2-x}}{x-1}$有意义,则x的取值范围是( )
| A. | x≤2 | B. | x≠1 | C. | x≤2或x≠1 | D. | x≤2且x≠1 |
6.若分式$\frac{|x|-3}{x-3}$的值为零,则x=( )
| A. | ±3 | B. | -3 | C. | 3 | D. | 0 |
3.若x=-1是关于x的一元二次方程ax2+bx-2=0(a≠0)的一个根,则2015-2a+2b的值等于( )
| A. | 2015 | B. | 2011 | C. | 2018 | D. | 2013 |
4. 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )| A. | 40° | B. | 50° | ||
| C. | 80° | D. | 随点B、C的移动而变化 |
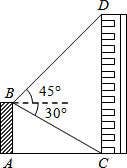 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7).
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度($\sqrt{3}$=1.7).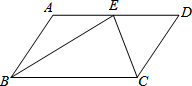 在?ABCD中,∠ABC和∠BCD的平分线交AD边上一点E,且BE=4,CE=3,求AD的长.
在?ABCD中,∠ABC和∠BCD的平分线交AD边上一点E,且BE=4,CE=3,求AD的长.