题目内容
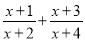 的和是________
的和是________
 【解析】试题分析:
=
=
=.
故答案为: .
【解析】试题分析:
=
=
=.
故答案为: .
练习册系列答案
相关题目
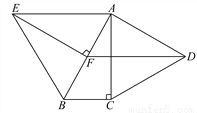
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为点F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
 (1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=...
(1)证明见解析(2)证明见解析
【解析】证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF =∠AEB= 30º,AE=AB,∠EFA= 90º.
∵∠ACB= 90º,∠BAC= 30º,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△AEF≌△BAC.
∴AC = EF.
(2)∵△ACD是等边三角形,
∴AC = AD,∠DAC=... 计算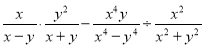
 【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式=
【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式= 分式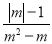 的值为零,则m取值为( )
的值为零,则m取值为( )
A. m=±1 B. m=-1 C. m=1 D. m的值不存在
 B
【解析】试题解析:分式的值为零的条件是分母不为0,分子为0,所以可以得到,可以得到, ,可以得到且,综上所述则m取值为-1
故选B.
B
【解析】试题解析:分式的值为零的条件是分母不为0,分子为0,所以可以得到,可以得到, ,可以得到且,综上所述则m取值为-1
故选B. 计算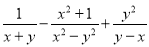
 【解析】试题分析:把y-x转化为-(x-y),x2-y2=(x+y)(x-y),最简公分母为x2-y2,通分后再相加减即可.
试题解析:
【解析】
原式=
=
=.
【解析】试题分析:把y-x转化为-(x-y),x2-y2=(x+y)(x-y),最简公分母为x2-y2,通分后再相加减即可.
试题解析:
【解析】
原式=
=
=. 计算 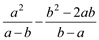 的值是___________
的值是___________
 【解析】试题分析:
=
=
=a-b.
故答案为:a-b.
【解析】试题分析:
=
=
=a-b.
故答案为:a-b. 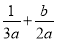 的结果是( )
的结果是( )
A. 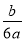 B.
B. 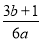 C.
C. 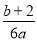 D.
D. 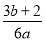
 D
【解析】试题分析:原式=
=.
故选D.
D
【解析】试题分析:原式=
=.
故选D. 甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )
A. 1℃~3℃ B. 3℃~5℃ C. 5℃~8℃ D. 1℃~8℃
 B
【解析】试题分析:设温度为x℃,由题意得,解得3≤x≤5,故答案选B.
B
【解析】试题分析:设温度为x℃,由题意得,解得3≤x≤5,故答案选B. 是否存在整数k,使方程组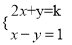 的解中,x大于1,y不大于1,若存在,求出k的值,若不存在,说明理由.
的解中,x大于1,y不大于1,若存在,求出k的值,若不存在,说明理由.
 k只能取3,4,5
【解析】【试题分析】解此题时可以解出二元一次方程组中x,y关于k的式子,然后解出k的范围,即可知道k的取值.
【试题解析】解方程组得
∵x大于1,y不大于1从而得不等式组
解之得2<k≤5
又∵k为整数
∴k只能取3,4,5
答:当k为3,4,5时,方程组的解中,x大于1,y不大于1.
k只能取3,4,5
【解析】【试题分析】解此题时可以解出二元一次方程组中x,y关于k的式子,然后解出k的范围,即可知道k的取值.
【试题解析】解方程组得
∵x大于1,y不大于1从而得不等式组
解之得2<k≤5
又∵k为整数
∴k只能取3,4,5
答:当k为3,4,5时,方程组的解中,x大于1,y不大于1. 
