题目内容
 如图,AB是⊙O的直径,点C在⊙O外,连接OC,OC⊥AB,弦BD交OC于点E,CD=CE
如图,AB是⊙O的直径,点C在⊙O外,连接OC,OC⊥AB,弦BD交OC于点E,CD=CE(1)求证:CD是⊙O的切线;
(2)若AB=13,BD=12,求DE的长.
考点:切线的判定,解直角三角形
专题:证明题
分析:(1)连接OD,如图1,由CD=CE得∠1=∠2,由CO⊥AB得∠3+∠5=90°,由于∠2=∠3,则∠1+∠5=90°,再加上∠4=∠5,所以∠1+∠4=90°,于是可根据切线的判定定理得到CD是⊙O的切线;
(2)连接AD,如图2,根据圆周角定理由AB是⊙O的直径得∠ADB=90°,在Rt△ABD中,根据勾股定理计算出AD=5,再证明Rt△BOE∽Rt△BDA,利用相似比可计算出BE=
,然后利用DE=BD-BE进行计算.
(2)连接AD,如图2,根据圆周角定理由AB是⊙O的直径得∠ADB=90°,在Rt△ABD中,根据勾股定理计算出AD=5,再证明Rt△BOE∽Rt△BDA,利用相似比可计算出BE=
| 169 |
| 24 |
解答: (1)证明:连接OD,如图1,
(1)证明:连接OD,如图1,
∵CD=CE,
∴∠1=∠2,
∵CO⊥AB,
∴∠3+∠5=90°,
而∠2=∠3,
∴∠1+∠5=90°,
∵OB=OD,
∴∠4=∠5,
∴∠1+∠4=90°,
∴OD⊥DC,
∴CD是⊙O的切线;
 (2)解:连接AD,如图2,
(2)解:连接AD,如图2,
∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△ABD中,
∵AB=13,BD=12,
∴AD=
=5,
∵∠OBE=∠DBA,
∴Rt△BOE∽Rt△BDA,
∴
=
,即
=
,
∴BE=
,
∴DE=BD-BE=12-
=
.
 (1)证明:连接OD,如图1,
(1)证明:连接OD,如图1,∵CD=CE,
∴∠1=∠2,
∵CO⊥AB,
∴∠3+∠5=90°,
而∠2=∠3,
∴∠1+∠5=90°,
∵OB=OD,
∴∠4=∠5,
∴∠1+∠4=90°,
∴OD⊥DC,
∴CD是⊙O的切线;
 (2)解:连接AD,如图2,
(2)解:连接AD,如图2,∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△ABD中,
∵AB=13,BD=12,
∴AD=
| AB2-BD2 |
∵∠OBE=∠DBA,
∴Rt△BOE∽Rt△BDA,
∴
| BE |
| AB |
| BO |
| BD |
| BE |
| 13 |
| ||
| 12 |
∴BE=
| 169 |
| 24 |
∴DE=BD-BE=12-
| 169 |
| 24 |
| 119 |
| 24 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
 已知:如图,线段a,
已知:如图,线段a,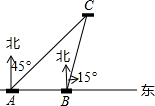 如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
如图,某日我国某岛附近海域有两艘自西向东航行的海监船A、B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
 已知∠β、∠γ与线段c,利用尺规
已知∠β、∠γ与线段c,利用尺规 如图,△ABC内接于⊙O,∠A=40°,则∠BOC=
如图,△ABC内接于⊙O,∠A=40°,则∠BOC=