题目内容
4.若数轴上的点M,N表示绝对值相等的两个数,并且这两个数之间的距离为7.2,若M点在N点的左侧,求M,N所表示的数,并在数轴上标出M,N的位置.分析 绝对值相等的两个数只有两种情况,相等或互为相反数,因为绝对值相等的两个数在数轴上对应的两个点的距离为7.2,所以这两个数是互为相反数的,可求得为±3.6.
解答 解:设其中一个数M为x,
因为两数绝对值相等,所以另一数N为-x,
由两个数在数轴上对应的两个点间的距离是8得,
|x-(-x)|=7.2,
解得:x=3.6或x=-3.6,
若M点在N点的左侧,
所以M=-3.6,N=3.6.
在数轴上表示如下:
点评 本题主要考查了绝对值在数轴上的定义(绝对值定义是坐标轴上的点到原点的距离),要求熟悉绝对值定义和数轴上数的规律.

练习册系列答案
相关题目
14.设a、b、c是实数,若a+b+c=2$\sqrt{a+1}$+4$\sqrt{b+1}$+6$\sqrt{c-2}$-14,则$\frac{a+c}{b+2a}$=$\frac{11}{3}$.
16.下列各项正确的个数为( )
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.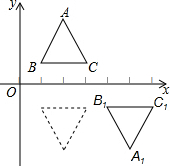 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
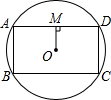 如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求:
如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求: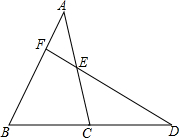 在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.
在△ABC中,点D在BC的延长线上,E是AC边中点,DE的延长线交AB于点F.